Astronomy 102 Specials: The Observer's Triangle

Astronomers make use of the ``Observer's Triangle'' when converting angles to distances. In the illustration below, the apparent size is the angular diameter of a planet (or any object), and if you know the distance to the planet, then trigonometry (yes, trigonometry) tells you the actual linear size of the planet:

where alpha is the angular size of the planet, D is its diameter, and R is the distance from Earth.

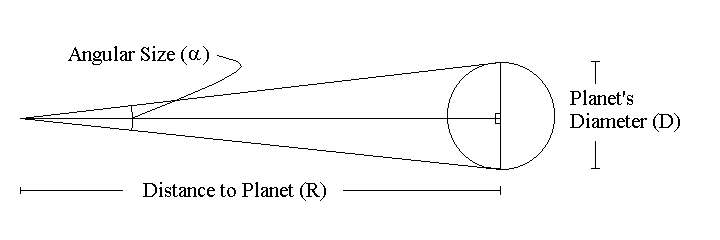
Now for those of you not particularly fond of trigonometry, the above equation is probably somewhat annoying, so just for you, I'm running a special on astrophysical assumptions which will simplify your life. In general, the objects astronomers observe are much farther away than they are big, so the Observer's Triangle is typically very skinny. An equivalent way to say this is that the angular size of astrophysical objects is typically quite small.

Because of the small angles involved, we can make an approximation which removes the need to calculate a tangent. Consider the illustration below, where two triangles are embedded within a circle whose radius is equal to the lengths of the long sides of each triangle:

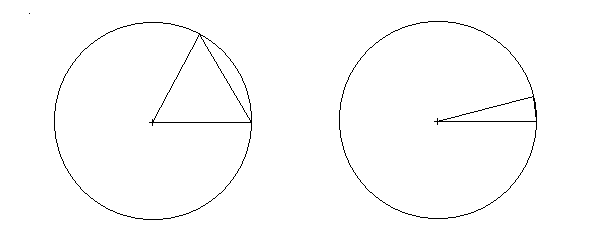
For the ``fat'' triangle, the length of the third side is quite different from the length of the part of the circle connecting the two long sides of the triangle. However, for the skinny triangle, the length of the third side is nearly equal to the length of the arc. For the skinny triangle, we can calculate the length of either the arc or the straight third side, and we'll get the same answer. Well, the length of the arc is pretty easy to calculate via some ratio arithmetic. We know that the circumference, C, of a circle is just

where R is the circle's radius, and that there are 360 degrees in a circle. Now we've changed our triangle to a pie slice, so the ratio of the angle of our slice, alpha, to 360 degrees should be the same as the ratio of the length of the pie slice's arc to the entire circumference. So,

or, moving the 2 x pi to the other side,

This approximation is accurate to 1% for angles smaller than 9 degrees, and since the angular diameter of the Moon (which has one of the largest angular extents of any object in the sky) is only one-half degree, we can make use of the approximation almost always in astronomy.

Back to the Astronomy 102 Specials Page