 |
Astronomy 101 Problem Set #10 Solutions |  |
 |
Astronomy 101 Problem Set #10 Solutions |  |
Problem #1: The Kuiper Belt is a collection of comet-sized junk which orbits the Sun with nearly circular orbits of typical radius 35 A.U. It is surmised that this reservoir of material is the source of the the so-called short period comets which occasionally transit the inner solar system. What is the period of the nearly circular orbits of these objects?
Solution: Oh no! It's the return of Kepler's Third Law! As you no doubt recall from the beginning of this course several eons ago, Kepler's Third Law is a relation between the period and semi-major axis of objects that orbit the Sun:
Hopefully, you also remember that in order to use this particularly simple expression of Kepler's Third Law, you need to express periods in years (Earth years, that is), and semi-major axes in A.U.
The problem tells us the radius of the nearly circular orbits of the Kuiper Belt objects is about 35 A.U., but this is a radius, not a semi-major axis, so what are we to do? Have no fear; just recall that a circle is a special case of an ellipse with eccentricity zero --- that is, the major and minor axes are the same size. Thus, for a circle the radius, major axis, and minor axis are all the same quantity, and therefore we can use 35 A.U. as the semi-major axis in this problem. So,
and so the period is the square root of this quantity,
Problem #2: In order for a Kuiper belt object to become a short period comet that enters the inner solar system, the eccentricity of its orbit has to change from about 0 to pretty close to 1. Suppose this magically happens, and the orbit of a Kuiper belt object changes from a nearly circular orbit with radius 35 A.U. to a highly elliptical orbit with eccentricity of nearly 1. Suppose further that the new orbit has aphelion (point farthest from the Sun) of 35 A.U., and perihelion (point closest to the Sun) of just 0.8 A.U.
a) What is the period of this new comet?
b) What is the eccentricity of his comet's orbit?
Hint: Draw a picture!
Solution: Let's start with the picture.
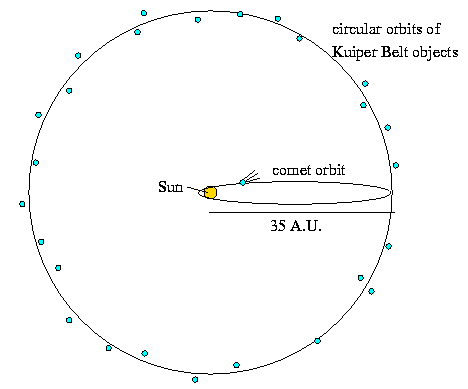
In the above picture, I've drawn the Kuiper Belt objects as little blue circles orbiting the yellow Sun with circular orbits (i.e., eccentricity = 0) at a distance of a 35 A.U. I've also drawn in the orbit of a highly eccentric comet (eccentricity = almost 1), whose perihelion is 0.8 A.U., and whose aphelion is 35 A.U.
Are these reasonable orbits for objects around the Sun? Recall Kepler's First Law, which states that objects in orbit around the Sun orbit in ellipses with the Sun at one focus. The circular orbits of the unperturbed Kuiper Belt objects satisfy this requirement, since the Sun is at the center of the circles, and since a circle (a.k.a. ellipse of eccentricity zero) has both foci located together at its center. Now what about this cometary orbit? We're told that the orbit has an eccentricity of nearly one, which means that f/a is nearly one, where f is half the distance between the ellipse's two foci, and a is the semi-major axis. Well, if f/a is nearly one, then the foci must be located pretty far from one another along the major axis. In the drawing above, I've put the Sun way down at one end of the major axis, and since Kepler said we need to have the Sun at one of the foci of an object's elliptical orbit, it looks like this cometary orbit satisfies his first law. Note: Do not put the Sun at the center of an elliptical orbit. It absolutely screams out that you do not understand Kepler Laws.
Now compare the comet's orbit and the circular orbits of the Kuiper belt objects in the diagram above. You should be able to convince yourself that the major axis of the comet's orbit is equal to the aphelion distance (35 A.U.) plus the perihelion distance (0.8 A.U.), which is much smaller than the major axis of the circular orbits. We need the comet's semi-major axis, so that's half of this value. Once you're convinced yourself that the comet's semi-major axis is half of 35.8 A.U., or 17.9 A.U., the remainder of the problem is the same as problem #1:
and so the period is the square root of this quantity,
Sounds pretty close to Comet Halley's 76 year period, doesn't it?
For part b), we need to calculate the eccentricity, which can be expressed as:
where a is the semi-major axis of the comet's orbit, and f is the distance between the center of the ellipse and either focus. We already know a, and getting f is pretty easy, since we already know the perihelion distance:
That means that the eccentricity is
Note that because the eccentricity is a ratio, it has no units.
Problem #3: Your textbook tells us that
there are approximately 1 million asteroids of diameter 1 km or
larger, and that together their mass is approximately 2% of the mass
of the Moon. If we assume that the "average" asteroid is a sphere with
diameter 10 km, then what is the average density of the "average"
asteroid? Express your answer in km/m3 so you can compare
it to densities you know. Based on this result, what do you think most
asteroids are made of?
Hint: Pretend that 1) all asteroids are exactly the same size and
density, 2) that there are 1 million of them, and 3) together they
account for the quoted mass.
Solution: This is an example of the kind of estimating astronomers do all of the time. In this case, we'll estimate the typical density of asteroids from knowledge of the mass of all of them, and a guess as to the size of a typical asteroid. We could instead measure the size and mass of each asteroid individually (though both measurements are really hard!), and then calculate a density for each one, but in most cases, we're more interested in an average value for the group than in each individual density.
For density, we need to know that mass and volume, so let's start by calculating the mass of the "average" asteroid. We're told that the mass of all of the asteroids together is about 2% of the mass of the Moon, which you can look up in your book:
But we're still not done with the mass calculation, though, since we want the mass of the "average" asteroid. The value above is the total mass of all the asteroids, but if that total is made up of one million "average" asteroids, then the mass of each average asteroid must be
Now let's calculate the volume of an "average" asteroid. We're told that the diameter is 10 km, which is 10,000 m. We want the radius, which is half of the diameter, or 5,000 m. So the volume is:
Now, the density is simply
This density is higher than that of water (1000 kg/m3) and less than that of iron (8000 kg/m3), and is pretty similar to that of normal everyday rock. Thus, we can conclude that asteroids are probably made of regular old rock.
