Bucknell Unversity Astronomy 101
Problem Set #2 Solutions

Problem #1: One night during a full Moon, you notice that the Moon subtends an angle of 0.46 degrees. Look up its size (be careful here) in the back of your book, and use it to calculate the distance to the Moon on that night.

Solution: This is a standard Observer's Triangle relation problem. We will do this same type of stuff many more times this semester.

Before we get started with the Observer's Triangle, however, we need to find the size of the Moon. That's in the Appendix on page 544 in the back of your textbook. There it says that the Moon's radius is 1738 km, or 1.738 x 106 m if I convert from km to m. We can set up the problem with a drawing like the one below:

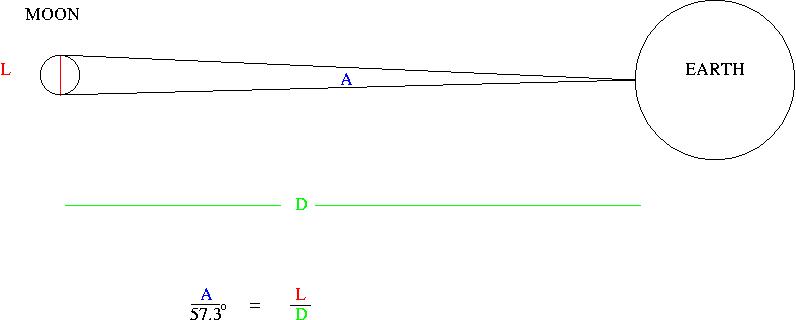
Note that for this problem, we need the diameter of the Moon, which is 2x its radius, or 2 x 1.738 x 106 m = 3.476 x 106 m.

Now, from the the Observer's Triangle relation above, and knowing that alpha = 0.46 degrees,

Now before we finish, let's subject this answer to a sanity check. First, check to see that the units make sense. A distance should be measured in meters or kilometers, or something that denotes length ( e.g., not degrees). Good. Now, we also can guess that the distance to the Moon is bigger than the size of the Moon. Is this answer bigger than the Moon's diameter, 3.476 x 106 m? Yep. OK. The result passes the sanity check. Do this. Always subject your answers to a sanity check. It can save your hide in an exam when the only mistake you made was some screwy unit conversion or flipping a fraction upside down.

The last thing we need to consider is how many significant digits to keep in our answer. To determine this, look at the number of significant digits in the inputs (i.e., the values you were given in the problem). We're told that the Moon subtends 0.46 degrees. That's 4.6 x 10-1 degrees, and there are two significant digits. The radius of the Moon in the back of the book is given to four significant digits, so how many significant digits should be in our answer? We can only know this answer to the same level of significance as our least significant input. That's the angle, which is given with only two significant digits. So our answer should have two significant digits.

Answer: The Distance to the Moon on this particular night is 4.3 x 108 m.

Note: The distance between the Earth and Moon changes because the Moon's orbit around the Earth is not a circle. If you answered 384,400 km, I know you cheated by looking up the distance in the back of the book.

Problem #2: At around 9:00 pm during this time of year, the star Vega appears almost directly overhead in our skies here in Lewisburg. If you were to call a friend in Santiago, Chile (which is nearly due south of here at a latitude of 33.5 degrees south) and asked him the altitude of Vega from his location, what would he say?

Solution: This problem is very much like last week's problem in that you're given the altitude of a star at one location and asked to calculate the altitude of that same star at another location.

It's really important to set up the problem graphically, and to make sure you've used all of the information available to you. Start by making a cutaway Earth drawing like we did last week. Put Lewisburg on your drawing in its proper position (latitude 41 degree north), and put in the vertical and horizontal directions. You're told that the star Vega is directly overhead in Lewisburg, so that means it has an altitude of 90 degrees. Draw in an arrow depicting the direction to Vega from Lewisburg. When you're done with this much, you should have a diagram that looks like this:

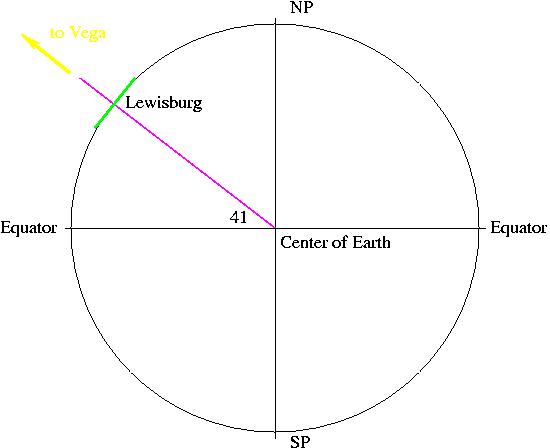
Now, let's put Santiago, Chile on the map. We're told that it's latitude is 33.5 degrees south, so it is south of the Equator, and we can place it on our diagram in the same way we placed Lewisburg:

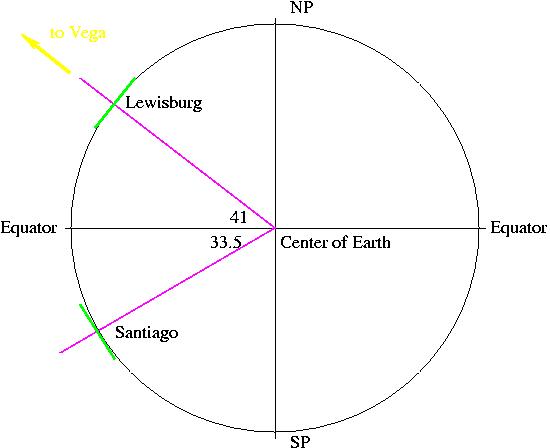
The last part of the setup involves drawing the direction to Vega from Santiago. This part should be easy by now, since no matter where you are on the Earth, the direction to a star is the same. Therefore, we can put in an arrow from Santiago pointing in the direction of Vega:

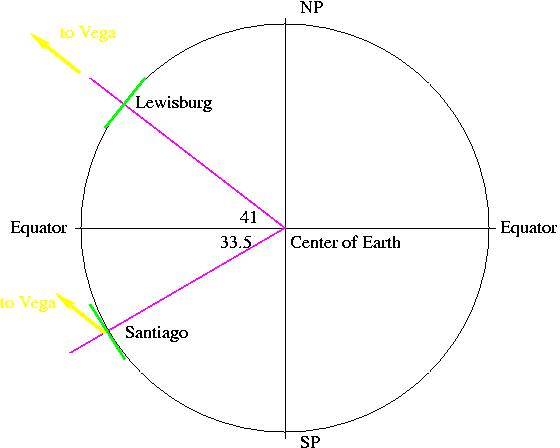
Now we're set up, and it's time to do some geometry. The angle we're looking for, labeled A in the diagram below, is the altitude of Vega above Santiago's northern horizon. As in problem 4 of Problem Set #1, we can make good use of parallel lines. Here, since the two yellow lines pointing to Vega are parallel, and the vertical direction at Lewisburg is also pointing in the same direction,the angle labeled B should be equal to 41+33.5, or 74.5 degrees.

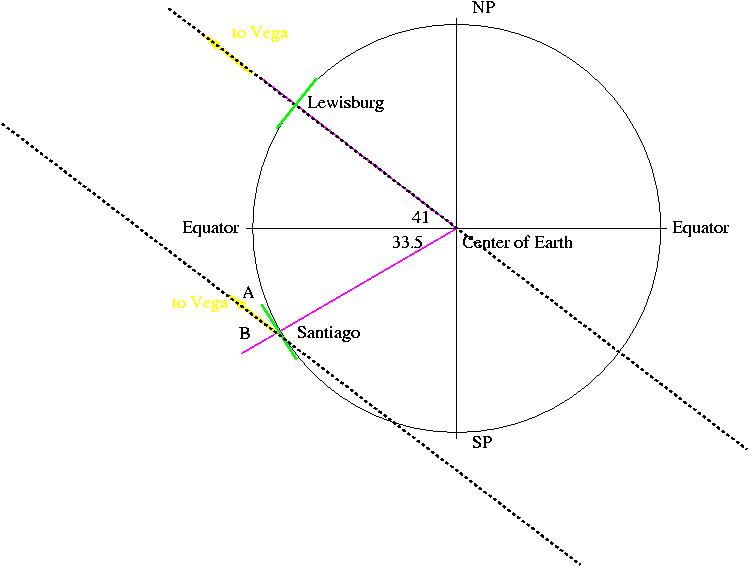
This really helps, since A+B is equal to the angle between the vertical and horizontal directions in Santiago, which of course must be 90 degrees. Thus,

and that means the altitude of Vega in Santiago is 15.5 degrees above the northern horizon.

Problem #3: The time interval between noon on 1 July and noon on 31 December is 183 solar days. How many sidereal days would that be?

Solution: I think that the easiest way to do this problem is to convert everything into minutes. We know that a solar day is 24 hours long, or

Therefore, 183 solar days is Now, a sidereal day is 23 hours and 56 minutes, or Therefore 183 solar days must be Why is this interesting? Well, 183 days is just about a half of a year, so the Earth has moved halfway around in its orbit during this time. Draw a diagram, and you should be able to convince yourself that at noon on 1 July, the part of the Earth you're on is pointing in nearly the opposite direction that it does on 31 December. In both cases, it's pointing toward the Sun, since the Earth has moved around the Sun. That's why it's been an integer number of solar days. However, since your part of the Earth isn't pointing in the same direction in space, this time interval cannot be an integer number of sidereal days. In fact, the Earth has had to go through 183 and a half rotations to get to this final position, and that's why the number of sidereal days isn't an integer.

Draw the diagram to convince yourself of this. Really. You'll thank me if you do. Honest.