Bucknell Unversity Astronomy 101
Problem Set #4 Solutions

Problem #1: In the spring of 2004, astronomers announced the discovery of a large, almost planet-sized rock deep in the outer reaches of our solar system. Some people have called this object the tenth planet, and have given it the name "Sedna." Sedna is about the size of Pluto, but it has an orbital period of 10500 years.

a) Calculate the semi-major axis of Sedna's orbit.

b) Astronomers have calculated that Sedna's "perihelion" distance (i.e., the closest it will ever get to the Sun) is 75 A.U. Based on this information, and the semi-major axis you calculated in part a), calculate the eccentricity of Sedna's orbit. (This is tricky -- try using some diagrams to help you make sense out of things. Note that a planet on an elliptical orbit is closest to the the Sun when it is at the "end" of the ellipse, i.e., crossing the line defined by the two foci.)

Solution: The first part is a classic plug-and-chug problem. No tricks at all. Just use Kepler's Third Law:

Period2 = (semi-major axis)3

Note here that Kepler's Third Law is strange in that the units don't come out right. The period must be in units of years and the semi-major xais must have units of A.U. This state of affairs results from the fairly mideval character of the law. A more modern writing would include a constant of proportionality, i.e.,

Period2 = k x (semi-major axis)3

where the k would have units of s2/m3. By using units of years and A.U., the constant K turns out to be 1.

If we use P2 = a3 where P is the period of Sedna in years and a is the semi-major axis of the orbit of Sedna in A.U., we get,

and because we set up Kepler's Third Law with units in years and A.U., our answer is

the semi-major axis of the orbit of Sedna is 479 A.U.

The second part of the problem requires you to remember what an ellipse looks like. Quite frankly, I can't imagine how you would do this problem without drawing a picture:

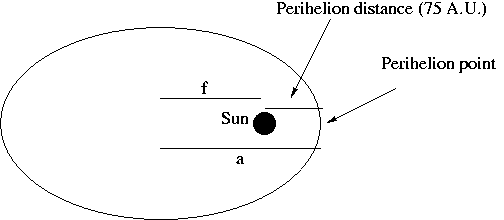
In the above figure, you can see Sedna's elliptical orbit about the Sun, which is located at one of the foci of the ellipse describing Sedna's orbit. The semi-major axis is indicated with the letter a, as is f, the distance between each focus and the center of the ellipse. Also indicated is the perihelion distance for Sedna. Sedna reaches it closest approach to the Sun at the "perihelion point" indicated.

Now that all of this stuff is defined, it should be pretty easy for you to see that f = a - 75 A.U., or 479-75 = 404 A.U. Why do we care about f? Because the eccentricity e is defined as

So now we can calculate the eccentricity. Note that the eccentricity is a ratio of two lengths, and as such has no units.

Problem #2: A couple of problems with wavelengths and frequencies:

a) That annoying beep on your microwave is actually a sound wave with frequency of about 3000 Hz. Assuming that the speed of sound waves is 330 m/s, calculate the wavelength of this sound wave.

b) Radio broadcasts from WVBU produce light waves with frequency 90.5 MHz ("mega"Hz, or "millions of Hz"). Calculate the wavelength of these waves. (Beware! Radio waves are light waves and do not travel at the speed of sound.)

Solution: Both sections of this problem are applications of the relationship between wavelength, frequency, and wave speed, i.e.,

wavelength x frequency = wave speed

In the first case, we're dealing with sound waves, which more (appropriately enough) at the speed of sound. So we can solve for the wavelength of the sound waves:

The number looks OK, but the units are awful. After all, this is supposed to be a wavelength, so the units should be some sort of length. The problem here is the pesky "Hz" unit. When we talk about a frequency of a wave, we are really asking how many waves per second are passing by us, and the unit "Hz" is shorthand for saying "per second." So 3000 Hz means 3000 waves per second. If we use this longhand way of writing the frequency, then our expression above looks like this: Well, there's a "/s" in each of the units in parentheses above, so we can cancel them out, and get for a final answer on, in words, "0.11 meters per wave," which is another way of saying that the wavelength is 0.11 meters.

For part b), the same process applies, but the wave speed is the speed of light, 3.00 x 108 m/s (RADIO WAVES ARE LIGHT WAVES!), and the frequency is 90.5 MHz, or 90.5 millions of Hertz , or 90.5 x 106 Hz. So we can again solve for the wavelength,

Problem #3: The Copernicus crater on the surface of the Moon has a diamter of 80 km.

a) If the moon is 3.84 x 105 km away, what is the angular size of the Copernicus crater?

b) Would you be able to resolve this crater with your eye (diameter= 5mm) in visible light (wavelength = 500 nm)?

Solution: The first part of this problem is the old Observer's Triangle once again. We've done a million of these by now, and if you're still having trouble with problems like this, we should talk.

In this case, we have an object (the Copernicus crater) whose linear size we know (80 km). We also know how far away it is (3.84 x 105 km), and we're asked for its angular size. So, using the Observer's Triangle relation:

The second part is a bit trickier, but provided you're actually doing the assigned reading, not much tricker. On page 128 of your textbook, you'll find the relationship which describes what minimum telescope size is required to see an object of specified angular size at a specified wavelength: where lambda is the wavelength in nanometers, alpha is the angular size in arcseconds, and D is the telescope size in centimeters. In order to use this equation, we'll need to convert our angular size from part a) into arseconds. Since there are 3600 arcseconds in one degree, Now we can figure out the minimum telescope size: OK -- so what does this result mean? It means that you'd need a telescope with a diameter or at least 0.23 cm to see the crater. Since our eyes have a diameter of 5mm, or 0.5 cm, they are in fact big enough to see this level of detail.