 |
Astronomy 101 Problem Set #8 Solutions |  |
 |
Astronomy 101 Problem Set #8 Solutions |  |
Problem #1: For a second, let's assume that there were canals on Mars running from the poles of the planet to thirsty cities in the equatorial regions. Let's further assume that these canals were very big, with widths of 10 km (that's huge: the Mississippi River is less than 2 km wide along virtually its whole length!).
a) If one were to observe Mars during an opposition (when it is only 0.52 A.U. from Earth), what would the angular width of these 10 km wide canals be?
b) The best Earth-based telescopes can barely distinguish structures with angular sizes of 1 arcsecond (1 arcsecond = 1/3600th of a degree). Would it be possible to see these canals with an Earth-based telescope?
c) How wide would the canals have to be if they could be observed with telescopes from Earth?
Solution: This is a direct application of the Observer's Triangle relation. If you had trouble with this problem, go back and read Lab #1 again. We want to know what angle an object (here a canal) of size 10 km will subtend when viewed from a distance of 0.52 A.U. First let's use common units. Change the A.U.'s to km:
Now we can use the Observer's Triangle relation
so,
So the canals on Mars will appear to be 7.36 x 10-6 degrees wide.
Ground-based telescopes can only see features larger than 1 arcsec, or 1/3600th of a degree, which is 2.78 x 10-4 degrees. Since the canals we imagined above have an angular width more than 10 times smaller than this, they never could have been seen with ground-based telescopes.
In order to be seen by telescopes on the Earth, the canals would need to have an angular size of 1 arcsecond, or 2.78 x 10-4 degrees. We can figure out how big they'd need to be physically by using the Observer's Triangle again, but "backwards" this time.
Problem #2: The Magellan spacecraft orbited Venus at an altitude of approximately 300 km (above its surface). Assume that the spacecraft's orbit was circular, and calculate its speed in its orbit. (Hint: You'll need to look up the mass and radius of Venus to answer this one.)
Solution: Here's a new twist on a speed calculation. In this case, you don't have a period, or any other time interval for that matter, so you can't use the reliable old speed = distance/time definition. This one requires a bit more thinking.
The Magellan spacecraft orbits Venus because of Venus' gravity. Without the gravitational pull from Venus, the spacecraft would fly along in a straight line and wouldn't turn as it does in a circular orbit.
The acceleration that the spacecraft feels due to the pull of Venus is
Now, since I also know that the Magellan spacecraft travels in a circle, I know that speed, acceleration, and orbital radius are related as follows:
Problem #3: Jupiter has an orbital period of 11.9 years.
a) Calculate the semi-major axis of its orbit.
b) Assuming that the orbits of both Jupiter and Earth are circular, calculate the minimum distance between these planets.
c) When Jupiter is as close to us as it ever gets, what is its angular size? (Hint: You'll need to look up Jupiter's radius for this one.)
Solution: OK, please tell me you know how to do part a) using Kepler's Third Law:
Drawing a diagram makes part b) very easy. Consider a picture of the orbits of Earth and Jupiter about the Sun:
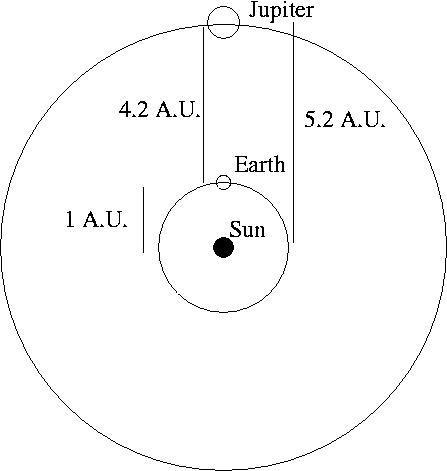
If the orbits are circular, it should be readily apparent to you that the two planets are closest to one another when they're "lined up" as in the above picture. I hope it's also obvious to you that when this occurs, the distance between them is 5.2 A.U. - 1 A.U. = 4.2 A.U.
Now, part c) is yet another Observer's Triangle problem. You now know how far away Jupiter is, so we only need the diameter of the planet. I found the radius in the back of our textbook, and doubled it to get a diameter = 1.43 x 105 km.
Converting 4.2 A.U. to km, I get,
Now I can use the Observer's Triangle relation,
so,
That's about 46 arcseconds.
