Astronomy 101 Specials: Aristarchus and the Size of the Moon

Part 1: Measuring the ratio of the size of the Moon to the size of the Earth's shadow at the Moon

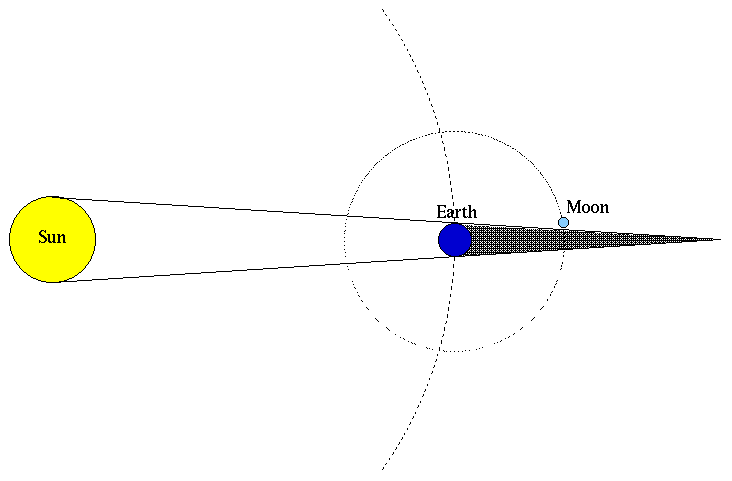
Aristarchus knew (as any natural philosopher at the time would have known), that on average twice a year, the surface of the full Moon became dark for a period ranging up to about two hours. It was correctly reasoned that during these times, the Moon was passing through the shadow cast by the Earth --- a lunar eclipse. The eclipse would only occur during the full Moon because that's the time when the Moon is on the opposite side of the Earth from the Sun. It didn't occur every time because the Moon's orbit and the Sun's orbit were tilted slightly relative to one another, so sometimes the Moon would pass above or below the Earth's shadow rather than right through it. Aristarchus realized that the longest lunar eclipses must occur when the Moon passes right through the center of the Earth's shadow, and furthermore, that the angular size of the Earth's shadow could be measured by noting the difference in the position of the Moon before and after the eclipse. He could then compare this angular size to the angular size of the Moon (which he could measure almost anytime) to get the ratio

angular size of Earth's shadow at the distance to the Moon
----------------------------------------------------------
angular size of the Moon

In addition, since the Moon and the Earth's shadow at the distance to the Moon are by definition at the same distance, the ratio of angular sizes is the ratio of physical sizes. (Remember the Observer's Triangle relation -- alpha/57.3 = D/R? For both triangles, R is the same, so the ratio of alpha's is equal to the ratio of D's)

Part II: Calculating the Size of the Earth's shadow at the distance to the Moon

Aristarchus could measure the angle labeled A in the drawing below, since it is one-half the angular size of the Earth's shadow at the distance to the Moon. He could also measure angle B, since that's one half of the angular size of the Sun, and this could easily be measured. From this information, he could calculate C, since A, B, and C together make a straight line, and therefore A + B + C = 180 degrees.

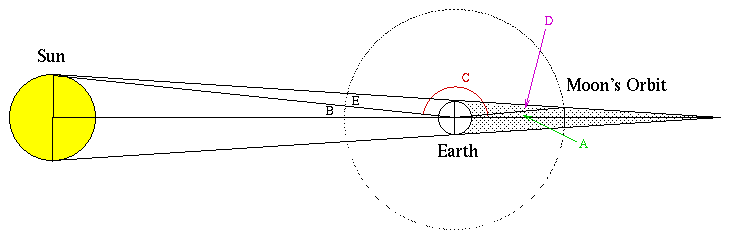
But C is also part of a triangle containing angles D and E, so C + D + E = 180 degrees, so,

A + B = D + E From the Observer's Triangle relation, we know that

A/57.3 = radius of the Earth's shadow at the distance to the Moon (R_em) / Earth-Moon distance (D_em)

B/57.3 = radius of the Sun (R_s) / Earth-Sun distance (D_es)

D/57.3 = radius of the Earth (R_e) / D_em

and, lastly

E/57.3 = R_e / D_es.

Combining all of these relations together, we get

R_em / D_em = R_e / D_es + R_e / D_em - R_s / D_es

Now just by coincidence, the angular sizes of the Sun and Moon were very nearly the same, and since they had the same angular sizes, the following relation was also true:

R_s / D_es = R_m / D_em

So, we can replace the last fraction in the big equation above and get

R_em / D_em = R_e / D_es + R_e / D_em - R_m / D_em

Multiplying through by D_em, we get

R_em = R_e x (D_em/D_es) + R_e - R_m

Now Aristarchus reasoned that the Sun was much farther away from the Earth than the Moon, so the fraction in the first term of the above equation would be very small (his own measurements showed this value to be 1/20; modern measurements of this value are 1/400). Therefore, he figured that the first term was negligble compared to the following two, and so

R_em = R_e - R_m

Part III: Putting Together Geometry and Observation to Measure the Size of the Moon

angular size of Earth's shadow at the distance to the Moon
---------------------------------------------------------- = 2.7
angular size of the Moon

which meant that

R_em/R_m = 2.7

but since

R_em = R_e - R_m

then

(R_e - R_m )/R_m = 2.7

and

R_e/R_m - 1 = 2.7

so

R_e = 3.7 x R_m.

Thus he propagated a terrestrial measurement (the radius of the Earth, which can be gotten easily from the circumference) to a celestial measurement.