



1) Why, if all objects feel the acceleration due to gravity toward the Earth, doesn't the Moon come crashing out of the sky and onto Earth?
and
2) Why, if as Galileo said, objects move with constant speed and direction until acted upon by an external force, does the Moon move in a circle rather than a straight line?
He quickly learned that the answer to each of these two puzzles was the other; that is, the Moon doesn't fall down to earth precisely because of its inertia and its orbital motion, and that it doesn't fly away from the Earth because of the earthward acceleration it feels.
Confused? Don't feel bad. It took Newton more than twenty years to figure this out (of course, he had to invent calculus along the way...). Let's look at it the way Newton did and see if, with the benefit of hindsight, we can understand it in a little less than twenty years.
Newton created an imaginary experiment, where a cannon was placed on a high mountaintop, and was fired horizontally. He knew that the distance the cannonball would travel horizontally in a time interval t would simply be its speed (v) times that time interval, e.g.,
(horizontal distance traveled in time t) = v x t
(ignoring air resistance and other real-world things that might slow it down; remember this is an imaginary experiment!). He also knew from Galileo's work with the acceleration due to gravity that the distance the cannonball would fall in the time interval t is
(vertical distance traveled in time t) = 1/2 a t2,
where a is the acceleration due to the Earth's gravity (we didn't spell out this formula in class, but well, there it is).
Newton looked at these two formulas for the distance a cannonball would travel horizontally and vertically, and he noticed that the distance the cannonball would fall in a given time interval t was constant, since a is constant. However, the distance the cannonball travels horizontally is dependent on its speed --- something he could control. So, if he changed the speed of the cannonball, he could change its trajectory, as illustrated below
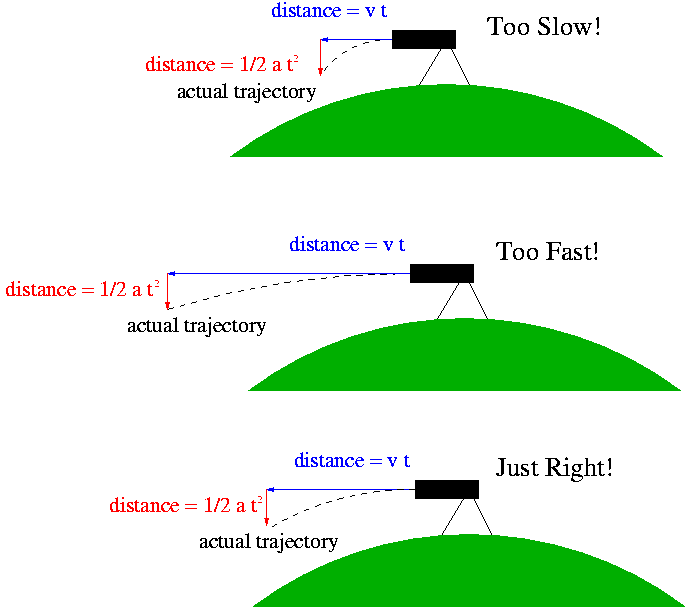
Then Newton realized that if he chose just the right velocity, the trajectory of the cannonball would curve at exactly the same rate the Earth (being spherical) curves, and therefore the cannonball would always stay the same height above the ground. In doing so, he balances the inertia of the cannonball (which makes it want to continue traveling in a straight line, and therefore away from the Earth) against the acceleration due to the Earth's gravity (which pulls the cannonball toward the center of the Earth).
The result is that the cannonball orbits the Earth, always accelerating toward the Earth, but never getting any closer. That may sound like a strange statement, but remember acceleration is the change in velocity, which is both the speed and direction of an object. In this case, the cannonball's direction is changing, and therefore it experiences an acceleration even though its speed doesn't change. (You experience this kind of acceleration when you go around a corner at constant speed in a car.)
Newton figured out that the speed of the cannonball was related to the acceleration due to the Earth's gravity (a) and the radius of the orbit (r; measured from the center of the orbit; i.e., the center of the Earth) as follows:
v2 = a x r
One cool thing about this relation is that even though Newton figured it out for a cannonball orbiting the Earth, it applies to any object in circular motion. Because of inertia, objects always want to travel in straight lines; in order to make them curve into circular motion, they have to be accelerated somehow. For Newton's cannonball, the Earth provided the acceleration. For a ball on a string, the tension in the string provides the acceleration. For your car going around a corner, the engine, through the tires and the friction between the tires and the road, provide the acceleration. In all cases, the amount of acceleration you'll need is described by the above equation, and is dependent on how fast the object is moving, and how tight a circular path it needs to travel on.