Astronomy 101 Specials: Measuring Distance via the Parallax Effect

The parallax effect is one of those things you see everyday and think nothing of until it's given some mysterious scientific-sounding name. There's really no magic here. Consider the following simple situation.

You're riding in a car on a highway out west. It's a beautiful sunny day, and you can see for miles in every direction. Off to your left, in the distance, you see a snow-capped mountain. In front of that mountain, and much closer to the car, you see a lone ponderosa pine standing in a field next to the highway. I've diagramed this idyllic scene in the figure below:

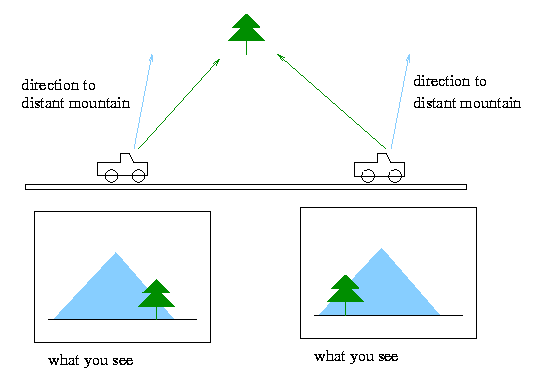
As you drive by the field, you notice an interesting sight. When you're in the position on the left side of the figure, the tree appears to be to the right of the mountain. You can see this in the figure by the fact that the line of sight to the tree (indicated by the green line) is rightward of the line of sight to the mountain (indicated by the blue line). A picture of what you see out the window of your car is shown below the car.

The interesting part is that as your drive on, you notice that the tree and mountain have switched positions; that is, by the time you reach the right hand position in the above figure, the tree appears to be to the left of the mountain. You can see this in the figure by noting that the line of sight to the tree (green line) is leftward of the line of sight to the mountain (blue line). A picture of what you see out the window of your car now is shown below the car.

What's going on here? It's pretty clear that the tree and mountain haven't moved at all, yet the tree appears to have jumped from one side of the mountain to the other. By now, you're probably saying "Well, DUH, the tree is just closer to me than the mountain. What's so remarkable about that?" I would answer, "There's nothing at all remarkable about it. It's just the effect of parallax." In fact, if you understand the above discussion, you already understand the parallax effect.

Now let's talk about measuring the distance to the tree using this information. From the above information, you can see that it would be pretty easy to measure the angle between the direction to the tree and the direction to the mountain in both instances. Let's call those angles A and B, respectively. Now, if the mountain is sufficiently distant so that the direction to the mountain from both viewpoints is the same, then the two blue lines in the figure below are parallel.

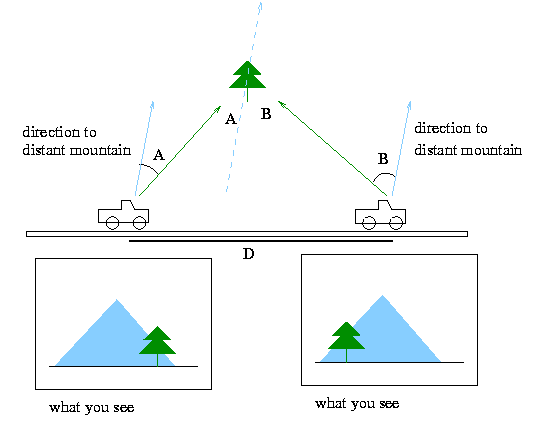
This helps a lot, because we can then show that the angle made by the two green lines (i.e., the difference in the direction to the pine tree from the two viewpoints) is equal to the sum of A and B. To see this, construct a line through the pine tree parallel to the two blue lines in the figure (this line is shown as a dotted line above). Then all of the blue lines are parallel, and each of the green lines crosses a pair of parallel lines. Reach deep back into your high school geometry (or equivalently, just stare at the above figure for a minute), and you'll remember or realize that the angles at the pine tree labeled A and B have the same values as the angles A and B measured at the two car positions. Thus, the angle between the two green lines is the sum of A and B, which are angles we can measure from the comfort of our car.

Now, if we know the distance D we've traveled, then we have an Observer's Triangle and we can solve for the distance to the tree using the Observer's Triangle relation

where alpha is the angle at the tree (A + B), D is the distance we've traveled between views, and R is the distance from the road to the tree.

This problem and solution can be directly extended to the astrophysical realm. In the diagram below, I've replaced the truck traveling on a road with the Earth orbiting the Sun, and I've replaced the tree and mountain with nearby and distant stars, respectively. B

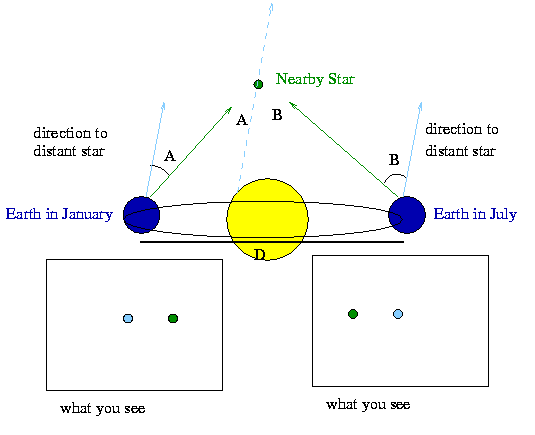
What you see in January are both stars, with the green one to the right of the blue one, as indicated in the "what you see" view at below left. However, six months later, the Earth has moved by 2 Astronomical Units to other side of the Sun, and now the pattern of nearby (green) and distant (blue) stars is reversed. Just as with the pine tree and mountain, the stars have not moved. They only appear in different relative positions in the sky because we have moved, and because one is nearer to us than the other.

Even though we've changed the scale by many orders of magnitude from the car picture to the orbiting Earth picture, the geometry remains the same, and therefore the method to calculate the distance to the nearby star is the same. We can measure directly the angles A and B from a photograph or image of the sky, and thereby get the angle between the two green lines which meet at the nearby star. Then, since we know the distance the Earth has traveled in the intervening six months, we can calculate the distance to the star using the Observer's Triangle relation.

so,

Now, the only cheat in all of this is that as you know, the Observer's Triangle relation really works only for small angles, and the way I've drawn the figures above, the angles don't look too small. However, when we apply this problem to the stars, we'll always have small angles, and we can always use the Observer's Triangle relation. For instance, the angles A and B for the nearest star to our solar system, Proxima Centauri, are less than 1 arcsecond, or 1/3600^th of a degree. I've just drawn these figures with larger angles, because it's just too hard to draw small angles and still make the diagrams look clear.

One last note: the term parallax when used for a star (i.e., the parallax of Alpha Centauri is ...) is a specific quantity. It is the angle through which as star appears to move (i.e., the sum of angles A and B in the diagrams above) for a baseline (i.e., D in the above diagrams) of 1 Astronomical Unit.

Back to the Astronomy 101 Specials Page