________________________________________
Name

EE 329: Take-Home Final Exam
May 7, 1997
Prof. Rich Kozick

Rules: You may use any books, notes, and computer software that you wish to complete this exam. (You will need to use Matlab for some problems.) However, you must work alone, and you are not permitted to discuss the exam with anyone. Please provide your answers on separate sheets of paper (not these pages). Data files for some problems are provided at the Final Exam link on the EE 329 home page.

Due Date: The exam is due by 8 AM on Tuesday, May 13.

Good luck, have fun, and have a good summer!

NOTE: FIGURES ARE OMITTED FROM THIS HTML VERSION.

Problem 1. (15 points)

Consider an analog signal x(t) whose frequency spectrum X(f) is non-zero only in the range from 900 Hz to 1100 Hz. For example, X(f) may have the shape shown below.

Suppose this analog signal is to be sampled in time.

a.

If the sampling rate is 2500 samples/second, is it possible to recover the original analog signal from the samples? Please explain the process that would be used. A sketch of the spectrum of the sampled signal and a block diagram of the digital-to-analog conversion process might be useful.

b.

Due to the ``band-pass'' nature of the signal, it is possible to sample at lower rates and still recover the analog signal. For example, a sampling rate of 500 samples/second can be used. Please explain why 500 samples/second is sufficient (you might start by sketching the spectrum of the sampled signal), and explain how the analog signal can be recovered from the samples.

Extra Credit: What is the lowest sampling rate from which the original analog signal can still be recovered? Explain your answer.

Problem 2. (10 points)

Download the file prob2.dat from the EE 329 home. The data in the file prob2.dat was obtained with a sampling rate of 100 samples/second. This data can be loaded into Matlab with the command

load prob2.dat -ascii

This data is known to consist of one or more sinusoidal components. Use the FFT to determine the number of distinct sinusoidal components that are present, the frequencies of those components, and the relative amplitudes of the components. Explain your approach and present data to support your conclusions.

(Hint: Zero-padding and windowing may be useful.)

Problem 3. (10 points)

Download the files prob3.m, prob3.x, prob3.y1, prob3.y2, prob3.y3, which simulate a radar signal processing problem. Radar operates by transmitting a signal and then ``listening'' for echoes from targets. When you run the Matlab script prob3.m, Figure 1 displays the signal x(n) that is transmitted. It consists of 10 repetitions of a pulse, where each pulse contains 2 cycles of a sine wave. The reason that 10 pulses are transmitted is that the echoes are often very weak, so the 10 pulses can be averaged to enhance the signal relative to noise.

When you run the Matlab script prob3.m, Figure 2 displays 3 separate received waveforms y1, y2, y3. The received waveform is either noise-only if no target is present, or signal plus noise. That is, the received waveform is either y(n) = w(n) where w(n) is Gaussian noise, or where x(n) is the transmitted signal, is the attenuation of the transmitted signal, and D is the delay that indicates the distance to the target. The noise is independent from sample to sample. Note in Figure 2 that the signal is strong enough in y1 to be visible. However, the presence or absence of the signal is not as clear in y2 and y3.

Your job is to determine for each of the 3 received signals whether the signal is present, and if the signal is present, what is the delay D. Explain the approach that you use, and present data to support your conclusions.

Problem 4. (10 points)

Suppose you are trying to determine the impulse response h(n) of a linear, time-invariant, causal, discrete-time system. You are able to measure the system output y(n) when the input is .

Is it possible to process y(n) in some way to obtain the impulse response h(n)? If so, explain exactly how y(n) should be processed to obtain h(n). If not, explain why.

Note: This question is similar to an earlier exam question, which asked how to obtain the impulse response from the step response. In that case, the answer was h(n) = y(n) - y(n-1). You should answer this question in a similar way, by providing a difference equation to obtain h(n) from y(n), if possible.

Problem 5. (15 points)

Use Matlab to design an FIR and an IIR digital filter to meet the following specifications:

High-pass filter
Sampling rate = 10,000 samples/second
Passband: 2,500 to 5,000 Hz
Stopband: 0 to 2,000 Hz
Passband ripple: less than 1 dB
Stopband attenuation: 40 dB or more

State the order and type of the FIR and IIR filters that you design. Verify that the specifications are achieved by plotting the frequency response of your filters.

Hint: For the IIR filter, you can use a function such as buttord to get information for a low-pass filter. Then you can modify this slightly to design IIR high-pass filters.

Problem 6. (10 points)

Design a first-order IIR digital high-pass filter using the bilinear Z transform (BZT). The digital filter should have 3 dB cutoff frequency (normalized) rad/sec. Base your digital filter on the high-pass analog filter transfer function

a.

Show the steps in your derivation of the digital filter. Plot the frequency response and verify that your filter meets the specification.

b.

Explain how this digital filter would be implemented in real-time. You might include a fragment of C code with your explanation.

Problem 7. (10 points)

This question asks you to determine a time signal x(n) from its DFT X(k). The time signal is sampled at samples/second, and N=1000 samples are recorded. The DFT values are X(100) = 1000(1 + j 1), X(900) = 1000(1 - j 1), and X(k) = 0 for all other k values in the range .

a.

What is the time signal x(n)?

b.

How are the amplitude, frequency, and phase of x(n) related to the DFT coefficients?

Answer this question using the definition of the DFT and inverse DFT, and not with Matlab:

Problem 8. (10 points)

Consider an FIR digital filter with the following properties: lowpass with cutoff rad/sec, N=21 coefficients , and symmetry in the coefficients of the form h(n) = h(N-1-n).

If the input to this filter is , what is the phase shift in the output signal?

Problem 9. (10 points)

The Wiener filter that we discussed in the context of noise cancellation can also be used to predict a time series. For example, some people might be interested in predicting the value that a stock will have in the future, based on the stock values during the past N days.

This problem can be stated as follows. Let y(k) for be the signal we want to predict (this is like the ``primary'' input in the noise canceler). Then define x(k) = y(k-1), which is like the ``reference'' input in the noise canceler. The objective is to predict y(k) from x(k), which means that we are trying to predict y(k) from past values of y(k).

As with the noise canceler, we can define the vector

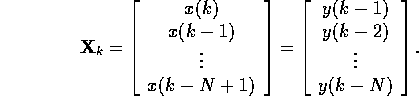
Then the Wiener filter with N coefficients

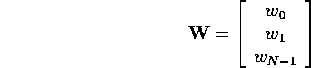
is used to form an estimate of the signal y(k) according to

so the predicted value is formed as a linear combination of the N past values
. The Wiener filter coefficients in are chosen to minimize the average squared error .

The Matlab program prob9.m derives the Wiener predictor , forms the predicted values , and plots the predicted values. Run the program for various values of N, beginning with N=1. What is the prediction for N=1? Is this reasonable? What happens as N is increased? Does the predictor perform ``well''? Are any segments of the signal better predicted than other parts? Why? Please try to explain what is happening in your own words.

 
• About this document ...