EE 329
Prof. Rich Kozick
Spring, 1997
Signals in the Time Domain and the Frequency Domain
The important idea from class on Friday, January 24
is to understand how to interpret the complex numbers
that arise in the frequency domain (Fourier transform)
representation of signals.
We looked at four signals, and their representations with
real sines/cosines and complex exponentials:
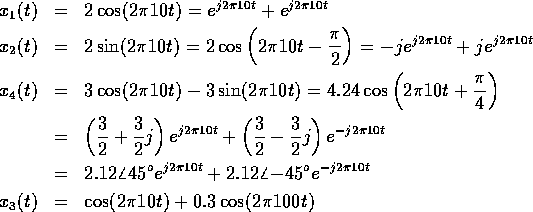
The complex coefficient D on the ``positive frequency''
exponential ![]() contains the following information:
(refer to
contains the following information:
(refer to ![]() for illustrations)
for illustrations)
Thus the complex value of a frequency component tells you the amplitude and the phase shift of the corresponding sinusoid that composes the time signal.