EE 329
Prof. Rich Kozick
Spring, 1997
EE 329: Homework Assignment #3
Date Assigned: Monday, February 10, 1997
Date Due: February 12 and 14, 1997
- Continue working on your FFT program as described on
the Lab 3 handout.
Submit your Matlab programs by Friday, February 14.
- Also for Friday,
explain why the computational complexity of the FFT algorithm
is
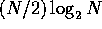 when
when 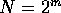 is a power of 2.
We showed in class that each butterfly requires 1 complex
multiply and 2 complex additions.
You should explain why
is a power of 2.
We showed in class that each butterfly requires 1 complex
multiply and 2 complex additions.
You should explain why 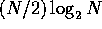 butterflies are needed.
butterflies are needed.
- Please work on the following problem for Wednesday,
February 12.
Bring your plots, ideas, and questions to class on Wednesday for
discussion. Then I will ask you to summarize your results and
submit them on Friday.
- Consider an analog signal that is a rectangular pulse described
by
x(t) = 1 for
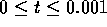 and x(t) = 0 otherwise.
Convince yourself that the Fourier transform of x(t) has magnitude
and x(t) = 0 otherwise.
Convince yourself that the Fourier transform of x(t) has magnitude
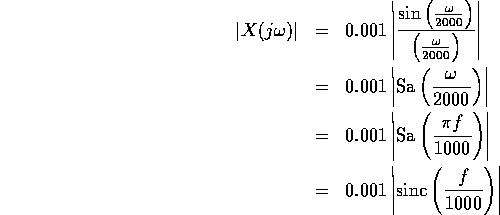
Sketch 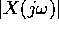 versus frequency f in hertz,
and plot using Matlab over the range
versus frequency f in hertz,
and plot using Matlab over the range 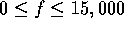 Hz.
Hz.
- Use the FFT to compute and plot the magnitude spectrum of
x(t).
Note that in order to use the FFT, the analog signal x(t)
needs to be sampled at some rate
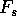 and with some number of
sampling points N.
What are the considerations in choosing
and with some number of
sampling points N.
What are the considerations in choosing 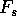 and N?
Try various values for
and N?
Try various values for 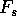 and N, and plot the FFT magnitude
spectra obtained with Matlab.
Try to explain the results that you are seeing.
Be sure to label the FFT spectra with hertz along the horizontal axis.
Can you obtain a spectrum with the FFT that is close to
the analytical result in part (a)?
and N, and plot the FFT magnitude
spectra obtained with Matlab.
Try to explain the results that you are seeing.
Be sure to label the FFT spectra with hertz along the horizontal axis.
Can you obtain a spectrum with the FFT that is close to
the analytical result in part (a)?
Kozick Rich
Sun Feb 9 18:02:20 EST 1997
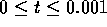 and x(t) = 0 otherwise.
Convince yourself that the Fourier transform of x(t) has magnitude
and x(t) = 0 otherwise.
Convince yourself that the Fourier transform of x(t) has magnitude
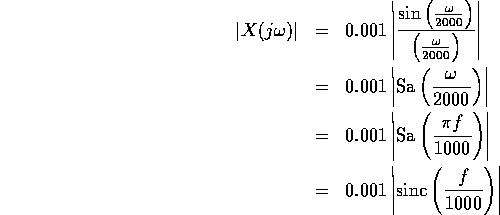
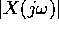 versus frequency f in hertz,
and plot using Matlab over the range
versus frequency f in hertz,
and plot using Matlab over the range 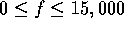 Hz.
Hz.
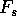 and with some number of
sampling points N.
What are the considerations in choosing
and with some number of
sampling points N.
What are the considerations in choosing 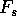 and N?
Try various values for
and N?
Try various values for 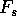 and N, and plot the FFT magnitude
spectra obtained with Matlab.
Try to explain the results that you are seeing.
Be sure to label the FFT spectra with hertz along the horizontal axis.
Can you obtain a spectrum with the FFT that is close to
the analytical result in part (a)?
and N, and plot the FFT magnitude
spectra obtained with Matlab.
Try to explain the results that you are seeing.
Be sure to label the FFT spectra with hertz along the horizontal axis.
Can you obtain a spectrum with the FFT that is close to
the analytical result in part (a)?