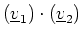We will not have class on Monday, March 21, because I will be in Philadelphia at a conference.
Recall also that we will have in-class Exam 2 on Wednesday, March 30, and this will be worth 12.5% of your grade. This exam will include the same topics as the take-home, plus sinusoidal steady-state analysis (phasors, frequency response, and filters).
- (a)
- For each sine wave, find the phasor representation
(in polar form), and sketch the phasor in the complex plane.
- (i)
-
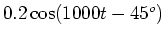
- (ii)
-
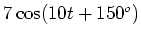
- (b)
- For each phasor, express the corresponding sine wave as
a time function, and sketch the sine wave versus time.
Assume
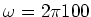 rad/sec.
rad/sec.
- (i)
-
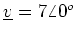
- (ii)
-
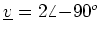
- (c)
- Find the magnitude of each complex number below.
- (i)
-
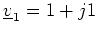
- (ii)
-
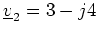
- (iii)
-
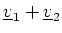
- (iv)
-