Chapter 2 Notes

Systems Modeled by Differential or Difference Equations

Continuous-time system with input x(t) and output y(t):

Many physical systems are accurately modeled by differential equations.

Example: RC circuit . Verify that the model is .

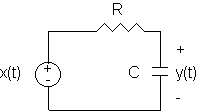
(You will model an RLC circuit for homework.)

Physical principles lead to differential equation models of systems: (see section 2.2 of the text)

• Electrical circuits: Voltage/current relations for capacitor and inductor, Kirchhoff's laws
• Mechanical systems: Position, velocity, acceleration relations and Newtons law
• Also fluid dynamics, thermal systems, chemical systems, and other applications

The general form of a linear differential equation model with constant coefficients is:

where the superscript indicates the number of derivatives of the function.

N is called the order of the system.
(Recall that earlier we referred to the RC circuit as a first-order filter.)

Need N initial conditions to get a complete solution. Why?

Important points and a preview of the rest of the course:

• Differential equations provide models for many systems that engineers work with.
• In MATH 212, you studied methods for solving the differential equations.
• In this course, we will develop several other tools for understanding systems: convolution, frequency response/Fourier transform, and transfer function/Laplace transform. These tools provide significant insight for system design.
• Example: In lab, we designed the RC circuit to function as a low-pass filter with cutoff frequency 1/(RC) rad/sec. Is it clear how to design such a filter using only the differential equation model? The tools of phasors and impedance provided considerable insight for filter design.
• Systems defined by differential equations of the form given above are linear and time-invariant if all initial conditions are zero. This can be proven with the same reasoning that we applied to the RC circuit in previous class notes.
• Zero-input response (ZIR) versus zero-state response (ZSR):

ZIR: Response to initial conditions only, with zero input x(t) = 0.
For many systems, the ZIR is transient and dies out with time.
Systems are nonlinear when the ZIR is considered. Why?

ZSR: Response to input x(t), with all initial conditions (or states) zero.
Many systems are linear and time-invariant with respect to the ZSR.
We will consider the ZSR almost always in this course: we will be concerned with how a system output is affected by the system input. (Most systems have inputs and outputs.)

ZIR and ZSR are related to (but slightly different than) the "homogeneous" and "particular" solutions to differential equations that you studied in MATH 212.

Discrete-Time Systems

Discrete-time system with input x[n] and output y[n]:

Consider the following two systems, which are examples of "digital filters":

1. y[n] = 0.5 ( x[n] + x[n-1] ) for n = 0, 1, 2, …
2. y[n] = 0.9 y[n-1] + x[n] for n = 0, 1, 2, …

Digital Filter Demonstration

What initial conditions are needed to compute the output sequence y[0], y[1], y[2], … ?

Difference equations are to discrete-time systems what differential equations are to continuous-time systems. The notes above regarding linearity, time-invariance, ZIR, and ZSR also apply to difference equations.

Discrete-time systems are becoming more common every day due to the trend toward digital processing. However, many physical systems and signals are continuous-time by nature. Thus we need to be comfortable with both continuous- and discrete-time systems and signals.

For systems 1 and 2, compute the output y[n] for the input x[n] shown below.

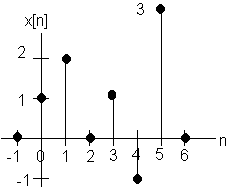
To prepare for convolution in Chapter 3: What is the "impulse response" h[n] of each system when the input x[n] is a "unit impulse" that equals 1 when n = 0 and equals 0 otherwise?

MATLAB program illustration: Computes and plots the output from systems 1 and 2 for the input x[n].