ELEC 320
Prof. Rich Kozick
Fall, 1997
Homework 15
Date Assigned: Wednesday, October 8, 1997
Date Due: Friday, October 10, 1997
Reading:
Sections 4.1 and 4.2 in the text on Fourier Series.
- 1.
- Please experiment with the
Simulink demonstration
of Fourier series that we used in class.
You can access the demonstration from the course home page
under Class Notes and Demonstrations.
You do not have to submit anything for this part.
- 2.
- In the Simulink demonstration
fsgen.m,
the three individual sine waves that are added together are
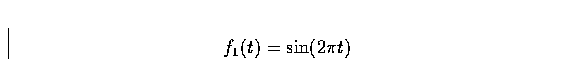
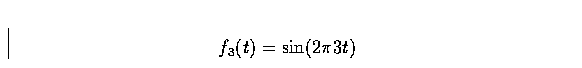
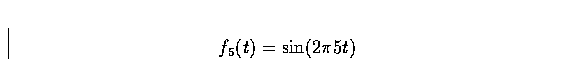
Compute the ``inner products'' of pairs of these sine waves over
the interval [0, 1].
That is, compute the following integrals:
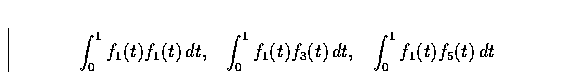
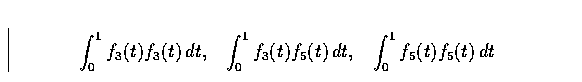
Some useful identities:
![\begin{displaymath}
\sin^2 a = \frac{1}{2} \left[ 1 - \cos (2a) \right], \;\;\;
...
...\sin b =
\frac{1}{2} \left[ \cos(a - b) - \cos (a + b) \right]\end{displaymath}](img6.gif)
You may find it useful to sketch the integrand in each case.
- 3.
- What does it mean geometrically when two vectors
have an inner product of zero?
Draw a picture of this situation in two dimensions.
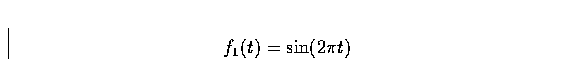
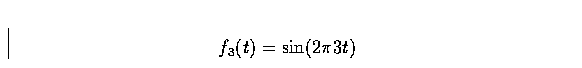
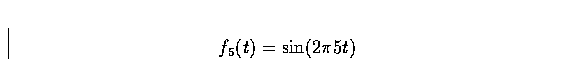
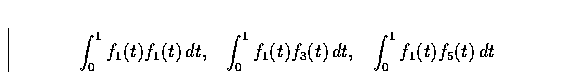
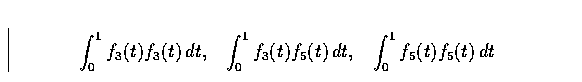
![\begin{displaymath}
\sin^2 a = \frac{1}{2} \left[ 1 - \cos (2a) \right], \;\;\;
...
...\sin b =
\frac{1}{2} \left[ \cos(a - b) - \cos (a + b) \right]\end{displaymath}](img6.gif)
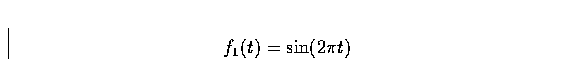
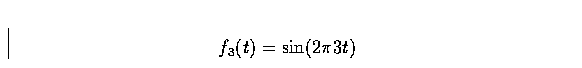
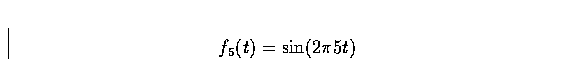
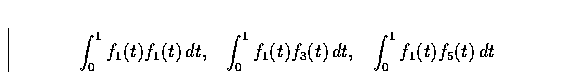
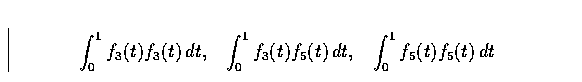
![\begin{displaymath}
\sin^2 a = \frac{1}{2} \left[ 1 - \cos (2a) \right], \;\;\;
...
...\sin b =
\frac{1}{2} \left[ \cos(a - b) - \cos (a + b) \right]\end{displaymath}](img6.gif)