Prof. Rich Kozick
ELEC 320, Fall 1997
Homework 20
Date Assigned: Monday, October 27, 1997
Date Due: Friday, October 31, 1997
- Quiz 4
will be on Monday, November 3, 1997.
- Reading:
Chapter 4 and Section 5.4 of Chapter 5.
- Lab Project:
Please submit a description of your lab project to me by email by Friday,October 31 at 9 AM. You will work on the projects next week.
- Find the steady-state output y(t) of the RC circuit below when the input is
x(t) = 1 + 0.5 cos (1000 t) + 0.25 cos (2000 t)
- A (low-speed) 100 bits/sec modem operates as follows. Bits are transmitted by sending
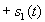 for a "1" and
for a "1" and 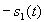 for a "0", where
for a "0", where 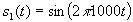 for
for 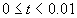 and
and 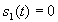 for other values of t. That is,
for other values of t. That is, 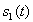 consists of 10 cycles of a 1000 Hz sine wave, so it lasts for 0.01 seconds. A sequence of bits is encoded as the signal
consists of 10 cycles of a 1000 Hz sine wave, so it lasts for 0.01 seconds. A sequence of bits is encoded as the signal 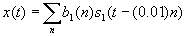 where n is an integer and each
where n is an integer and each 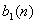 is either +1 or -1.
is either +1 or -1.
The receiver uses a matched filter that integrates over 0.01 seconds:
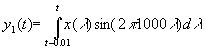 and whose output is sampled every 0.01 seconds.
and whose output is sampled every 0.01 seconds.
What is the matched filter output when a "1" is transmitted and when a "0" is transmitted?
Now suppose that we want to send 200 bits/sec. We can define another pulse
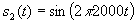 for
for 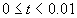 and
and 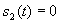 for other values of t. Then a different bit sequence
for other values of t. Then a different bit sequence 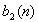 can be transmitted at the same time as
can be transmitted at the same time as 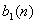 using the signal
using the signal
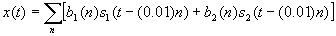
How should x(t) be processed to recover both bit sequences 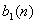 and
and 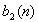 ? Can you define a second matched filter that will detect
? Can you define a second matched filter that will detect 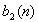 ? Explain your reasoning.
? Explain your reasoning.
Hint: What is 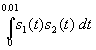 ?
?
- Use the table of Fourier transform pairs and theFourier transform properties to answer items 6-9. Do problem 4.12(a), and find the Fourier transform of the signals x(t) and y(t) shown below.
- The signal transmitted in an ultrasound imaging system is typically a "sine wave burst" of the form
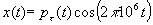 . This is a 1 MHz cosine that is "on" for
. This is a 1 MHz cosine that is "on" for 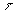 seconds.
seconds.
(a) For 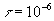 sec, sketch x(t), then find and plot
sec, sketch x(t), then find and plot 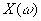 .
.
(b) Repeat part (a) for 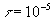 .
.
(c) Which case of signal would you call "narrowband", and which is "wideband"?
You might want to use MATLAB to produce the plots. An example is on page 164 of the text.
- Problem 5.28. Hints:
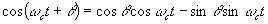 and
and 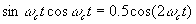 .
.
- Suppose we model a telephone channel as an ideal low-pass filter with cutoff frequency 4000 Hz, as shown in the frequency response
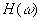 shown below.
shown below.
(a) What is the impulse response of this filter?
Is this a causal system?
(b) What is the filter output y(t) when the input is 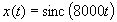
? Find and sketch y(t).
Extra credit: What is the filter output y(t) when the input is a rectangular pulse
Thank you.
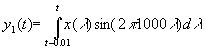 and whose output is sampled every 0.01 seconds.
and whose output is sampled every 0.01 seconds.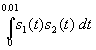 ?
?