ELEC 320
Prof. Rich Kozick
Fall, 1998

ELEC 320: Homework Assignment 16

Date Assigned: 		 Monday, November 2, 1998 
Date Due: 		 Wednesday, November 4, 1998

Reading: Chapter 4, Sections 4.3 and 4.4.

Lab: Please decide on a lab project by November 5 and 10 so that we can begin working on them.

Problems:

1.

Please study Example 4.7 in the text on pages 166-167. Do your best to write down all of the steps required to show that the Fourier transform of a rectangular pulse is a ``sinc'' function. This is one of the most important Fourier transform pairs to understand - it arises in many applications. You do not have to submit anything for this item.

2.

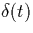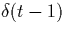Find the Fourier transform of the functions $\delta(t)$ and $\delta(t-1)$ using the definition of the Fourier transform, not the table. In other words, compute the integral that defines the Fourier transform for these time functions. (Hint: Recall the ``sifting'' property of impulse functions.)

3.

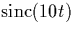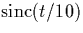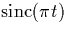Sketch ${\rm sinc}(10t)$, ${\rm sinc}(t/10)$, and ${\rm sinc}(\pi t)$.Label the amplitude at t=0 and the zero-crossing points.

4.

Sketch 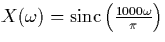$X(\omega) = {\rm sinc}\left( \frac{1000 \omega}{\pi} \right)$.Find the inverse Fourier transform x(t) using the tables, and sketch x(t).

5.

What is the Fourier transform of 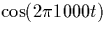$\cos(2 \pi 1000 t)$? Sketch the 2-sided amplitude spectrum.