ELEC 320
Prof. Rich Kozick
Fall, 1998
Homework 2
Date Assigned: Friday, August 28, 1998
Date Due: Monday, August 31, 1998
Reading:
We will discuss Chapter 1 in the Kamen/Heck text next week.
Please start reading Chapter 1 as follows:
section 1.1, browse sections 1.2-1.4, and read section
1.5.
Problems:
Please work on the following problems for Monday.
Do your best to solve the problems, and come to class with questions.
We will review the solutions in class on Monday.
- 1.
- Consider the low-pass RC circuit filter that we discussed in
class, which is shown below.
[CIRCUIT DIAGRAM OMITTED IN HTML VERSION]
- (a)
- What is the formula for the ``complex frequency response''
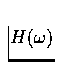 ?
?
- (b)
- What are the formulas for the magnitude
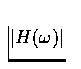 and the phase
and the phase 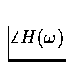 of the frequency response?
of the frequency response?
- (c)
- For the values R=1.1
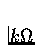 and C=0.22
and C=0.22 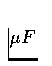 considered in class, produce rough sketches of
considered in class, produce rough sketches of
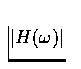 and
and 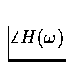 versus
versus 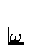 .What is the ``amplitude gain'' of the circuit at low frequencies?
.What is the ``amplitude gain'' of the circuit at low frequencies?
- (d)
- Use your formula for
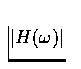 and the definition of
cutoff frequency
and the definition of
cutoff frequency 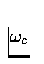 to derive an expression
for
to derive an expression
for 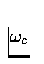 as a function of R and C.
This is the expression that is required in order to design
a filter (i.e., choose R and C) to achieve a specified
cutoff frequency.
Hint: The cutoff frequency
as a function of R and C.
This is the expression that is required in order to design
a filter (i.e., choose R and C) to achieve a specified
cutoff frequency.
Hint: The cutoff frequency 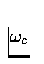 is defined as the value
of frequency that produces amplitude gain
is defined as the value
of frequency that produces amplitude gain 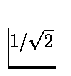 , i.e.,
, i.e.,
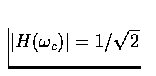 .
.
- 2.
- Please answer the same questions for the RC circuit shown below.
What type of filter is this circuit (low pass, high pass, or band
pass)?
[CIRCUIT DIAGRAM OMITTED IN HTML VERSION]
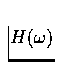 ?
?
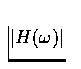 and the phase
and the phase 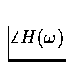 of the frequency response?
of the frequency response?
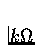 and C=0.22
and C=0.22 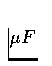 considered in class, produce rough sketches of
considered in class, produce rough sketches of
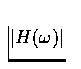 and
and 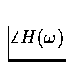 versus
versus 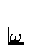 .What is the ``amplitude gain'' of the circuit at low frequencies?
.What is the ``amplitude gain'' of the circuit at low frequencies?
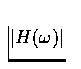 and the definition of
cutoff frequency
and the definition of
cutoff frequency 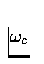 to derive an expression
for
to derive an expression
for 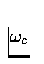 as a function of R and C.
This is the expression that is required in order to design
a filter (i.e., choose R and C) to achieve a specified
cutoff frequency.
Hint: The cutoff frequency
as a function of R and C.
This is the expression that is required in order to design
a filter (i.e., choose R and C) to achieve a specified
cutoff frequency.
Hint: The cutoff frequency 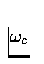 is defined as the value
of frequency that produces amplitude gain
is defined as the value
of frequency that produces amplitude gain 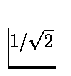 , i.e.,
, i.e.,
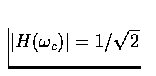 .
.