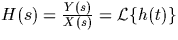ELEC 320: Review for Final Exam
Fall, 1998
Prof. Rich Kozick
The final exam is on
Thursday, December 10, 1998 at 8:00 AM in room COLEMAN 252.
The exam will be closed-book and closed-notes, except that you
can bring one sheet of 8.5 inch by 11 inch paper containing any notes
that you would like.
Important formulas and transform tables will be provided for you.
The following is a list of important concepts from the course.
You should understand what each concept means, why it is important, and
how to use it to solve problems.
- Analog filters (Lab 1 and other times during course):
- Frequency response and Bode plot
- Phasors and impedance
- Amplitude gain, decibels (dB), and phase shift of a filter
- 3 dB cutoff frequency of a filter
- Filter types: low-, high-, band-pass, and band-stop
- ``Order'' of a filter
- Signals and systems:
- Continuous- versus discrete-time
- Classifying systems as linear, time-invariant, and causal
- Linear systems: understand the definition and how to apply it
- Systems modeled by differential and difference equations
- Systems in the time-domain:
- Impulse function and impulse response of a system
- Convolution: why important, why true, how to compute
- Frequency analysis of signals and signal processing:
- Fourier series: what it means, how to compute (using
formulas), how to apply (periodic signal through a filter ...)
- Amplitude and phase spectra of signals
- Fourier transform:
what it means, how to compute using tables of transform pairs and
properties
- Applications: Amplitude modulation, linear systems and frequency
response, sampling theorem (minimum sampling rate,
digital-to-analog conversion)
- Systems in the s-domain:
- Laplace transform: use tables of transform pairs and
properties to compute forward and inverse transforms.
Perform partial fraction expansions analytically for cases with
real and distinct roots, and be able to apply results of
the MATLAB residue command for more complicated cases.
- Transfer function: definitions
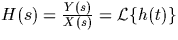
- Poles and zeros of a system
- Relation between poles and zeros of H(s) and the frequency
response of a filter (??)