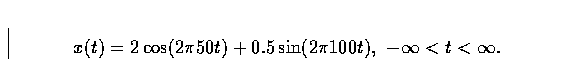ELEC 470, Spring 1998
Prof. Rich Kozick

Homework 4


Date Assigned: Monday, February 2, 1998
Date Due: Monday, February 9, 1998

  1. Please begin reading Chapter 3 for Friday, particularly Sections 3.1 - 3.3.

  2. Remember that Project 1 is due on Wednesday, February 4. Be sure to explain your reasoning in the writeup that you submit.

  3. You are given two data files, sig1.dat and sig2.dat, which can be downloaded from the Web page for this assignment. These are both ASCII files, and they can be loaded into Matlab with the command
    load sig1.dat -ascii
    after which a variable named sig1 will be available. (The same can be done with sig2.dat.) Both files were recorded by sampling a signal at a rate of 60 samples per second.

    Analyze the frequency content of these data files using the FFT in MATLAB. For each data file, how many sine waves appear to be present? What are the frequencies of the sine waves? Can you say anything about the relative amplitudes of the various sine wave components?

  4. A Java applet that graphically illustrates continuous-time convolution is available at
    http://spectrum.ece.jhu.edu/wjr/
    with the title "Joy of Convolution". You should check it out as a review of the process of convolution. (Nothing needs to be handed in for this part.) You might want to browse the other demonstrations at this site to review other topics in signals and systems.

  5. Consider a linear, time-invariant system with impulse response h(t) shown below.


    \begin{figure} \centerline{ \epsfxsize=5.5in \epsfysize=2in \epsfbox{hw4fig.eps}}\end{figure}

    (a) What is the expression for h(t) in terms of the rect function?

    (b) Sketch the output signal y(t) from the system when the input signal is x(t) as shown above.

    (c) What is the frequency response H(f) of this system? Sketch the amplitude response |H(f)|.

    (d) Find the steady-state system output y(t) when the input is

    \begin{displaymath} x(t) = 2 \cos (2 \pi 50 t) + 0.5 \sin (2 \pi 100 t), \,\, -\infty < t < \infty.\end{displaymath}

    Hint: Is it simpler to find the output in the time domain or the frequency domain?

  6. Consider the RC circuit shown below with R = 1000 ohms and C = 1e-6 farads. Please find the frequency response H(f), and sketch the amplitude and phase response of the filter for frequencies in the range 0 Hz to 10,000 Hz.

    \begin{figure} \centerline{ \epsfxsize=2.5in \epsfysize=1.7in \epsfbox{hw4rc.eps}}\end{figure}

  7. What is the frequency response H(f) of a system that whos output is the Hilbert transform of the input signal?

  8. In the single sideband (SSB) demonstration program hilbert_demo.m that we discussed in class, how can the original signal g(t) = sinc(t) be recovered from the SSB modulated signal? Please draw a block diagram of a system that will output g(t).
Thank you.