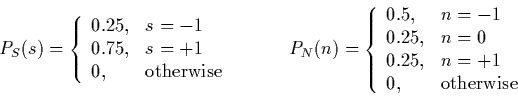
- (a)
- Suppose the receiver obtains the value X = x.
Find the signal estimate
 that minimizes
the mean-squared error
that minimizes
the mean-squared error ![$E [ ( S - \hat{s}(x))^2]$](img3.gif) .Show all of the steps in your analysis, and display
.Show all of the steps in your analysis, and display
 as a plot versus x.
I suggest that you draw plots of
PS(s), PN(n), PX,S(x,s), PX(x),
PS|X(s|x) as we did in class.
as a plot versus x.
I suggest that you draw plots of
PS(s), PN(n), PX,S(x,s), PX(x),
PS|X(s|x) as we did in class.
- (b)
- How would you process the signal estimates
 in order to recover the binary values
in order to recover the binary values
 of S?
In other words, what ``decision rule'' would you use to recover
the bits from X based on
of S?
In other words, what ``decision rule'' would you use to recover
the bits from X based on  ?
?
- (c)
- For the decision rule that you developed in part b, what is the probability of a bit error for this system? Explain your reasoning.
- (d)
- Write a MATLAB program to simulate this system,
including the decision rule developed in part b.
Compare the bit error rate (BER) in your simulation with the
analytical probability of a bit error computed in part c.
Be sure to compare the simulated and analytical BER!

- (a)
- Find the marginal PMFs PX(x) and PY(y), and plot them.
- (b)
- Find the mean and variance of X and Y:
 .
. - (c)
- Find the correlation between X and Y, defined as rX,Y = E [ X Y].
- (d)
- Find the covariance
![${\rm Cov} [ X, Y ]$](img6.gif) .
. - (e)
- Find the correlation coefficient
 .
. - (f)
- Are X and Y independent random variables? Recall that X and Y are independent if and only if PX,Y(x,y) = PX(x) PY(y).
- (g)
- Find the conditional PMFs
PX|Y(x|y) = P [ X = x | Y = y]
PY|X(y|x) = P [ Y = y | X = x]
and plot each of these versus x and y (on separate plots). - (h)
- Suppose you need to produce an estimate
 of X
that minimizes the mean squared error
of X
that minimizes the mean squared error ![$E [ (X - \hat{x})^2 ]$](img9.gif) .You must do this with no information about Y.
What value should you choose for
.You must do this with no information about Y.
What value should you choose for  , and why?
(Your answer should be a number!)
, and why?
(Your answer should be a number!)
- (i)
- Suppose that you observe that the random variable
Y takes on the value y (i.e., Y = y).
We would like to incorporate the knowledge that Y=y to improve
our estimate of X.
For each possible value of y, what is your estimate of X,
denoted by
 ?
Explain how to compute
?
Explain how to compute  , and present a plot of
, and present a plot of
 versus y.
versus y.
- (j)
- Is
 in part (i) different from
in part (i) different from  in part (h)?
Is this reasonable based on the probability values in the joint PMF?
Is this reasonable based on the value of correlation coefficient
in part (h)?
Is this reasonable based on the probability values in the joint PMF?
Is this reasonable based on the value of correlation coefficient
 that you computed in part (e)?
That is, does the value of
that you computed in part (e)?
That is, does the value of  lead you to expect
that information about Y should be useful in predicting the
value of X?
lead you to expect
that information about Y should be useful in predicting the
value of X?
- (k)
- Using your answers from parts (h) and (i), compute the
following quantities:
![$E [ (X - \hat{x})^2 ]$](img9.gif) ,
,
![$E[(X-\hat{x}(-1))^2 \vert Y=-1]$](img11.gif) ,
,
![$E[(X-\hat{x}(0))^2 \vert Y=0]$](img12.gif) , and
, and
![$E[(X-\hat{x}(1))^2 \vert Y=1]$](img13.gif) .Do these results show that we get better estimates for X
when the value of Y is known? Please explain.
.Do these results show that we get better estimates for X
when the value of Y is known? Please explain.