ELEC 471
Prof. Rich Kozick

Homework 9

Date Assigned: Thursday, April 5, 2001
Date Due: Thursday, April 12, 2001

Reading: Please read Chapter 4, Sections 4.1 - 4.5.

1.

In this problem, I would like you to perform an analysis of a digital communication system that is similar to the case that we studied in class on April 5. The only difference is that the signal S and noise N have PMFs as follows.

$$P_S(s) = \left\{ \begin{array} {ll} 0.25, & s = -1 \ 0.75, ... ... 0 \ 0.25, & n = +1 \ 0, & {\rm otherwise}\end{array} \right.$$

The random variables S and N are independent. The receiver observes the random variable X = S + N.

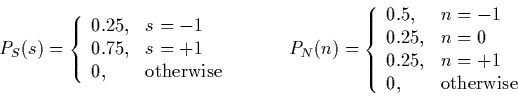
(a)

Suppose the receiver obtains the value X = x. Find the signal estimate $\hat{s}(x)$ that minimizes the mean-squared error $E [ ( S - \hat{s}(x))^2]$.Show all of the steps in your analysis, and display $\hat{s}(x)$ as a plot versus x. I suggest that you draw plots of P_S(s), P_N(n), P_X,S(x,s), P_X(x), P_S|X(s|x) as we did in class.

(b)

How would you process the signal estimates $\hat{s}(x)$ in order to recover the binary values $\{ -1, +1 \}$ of S? In other words, what ``decision rule'' would you use to recover the bits from X based on $\hat{s}(x)$?

(c)

For the decision rule that you developed in part b, what is the probability of a bit error for this system? Explain your reasoning.

(d)

Write a MATLAB program to simulate this system, including the decision rule developed in part b. Compare the bit error rate (BER) in your simulation with the analytical probability of a bit error computed in part c.

Be sure to compare the simulated and analytical BER!

2.

Please answer the following questions for the joint PMF P_X,Y(x,y) shown in the figure below.

(a)

Find the marginal PMFs P_X(x) and P_Y(y), and plot them.

(b)

Find the mean and variance of X and Y: $\mu_X, \mu_Y, \sigma_X^2, \sigma_Y^2$.

(c)

Find the correlation between X and Y, defined as r_X,Y = E [ X Y].

(d)

Find the covariance ${\rm Cov} [ X, Y ]$.

(e)

Find the correlation coefficient $\rho_{X,Y}$.

(f)

Are X and Y independent random variables? Recall that X and Y are independent if and only if P_X,Y(x,y) = P_X(x) P_Y(y).

(g)

Find the conditional PMFs

P_X|Y(x|y) = P [ X = x | Y = y]

P_Y|X(y|x) = P [ Y = y | X = x]

and plot each of these versus x and y (on separate plots).

(h)

Suppose you need to produce an estimate $\hat{x}$ of X that minimizes the mean squared error $E [ (X - \hat{x})^2 ]$.You must do this with no information about Y. What value should you choose for $\hat{x}$, and why? (Your answer should be a number!)

(i)

Suppose that you observe that the random variable Y takes on the value y (i.e., Y = y). We would like to incorporate the knowledge that Y=y to improve our estimate of X. For each possible value of y, what is your estimate of X, denoted by $\hat{x}(y)$? Explain how to compute $\hat{x}(y)$, and present a plot of $\hat{x}(y)$ versus y.

(j)

Is $\hat{x}(y)$ in part (i) different from $\hat{x}$ in part (h)? Is this reasonable based on the probability values in the joint PMF? Is this reasonable based on the value of correlation coefficient $\rho_{X,Y}$ that you computed in part (e)? That is, does the value of $\rho_{X,Y}$ lead you to expect that information about Y should be useful in predicting the value of X?

(k)

Using your answer from part (h), compute $E [ (X - \hat{x})^2 ]$

Using your answer from part (i), compute following quantities:
$E[(X-\hat{x}(-1))^2 \vert Y=-1]$, $E[(X-\hat{x}(0))^2 \vert Y=0]$, and
$E[(X-\hat{x}(1))^2 \vert Y=1]$.

Do these results show that we get better estimates for X when the value of Y is known? Please explain.

Presentations: The following students are asked to present their solution to these problems. The presentation will be done as a group.

Item 1
Shawn Mattews and Matt Murdock

Item 2
Kevin Murphy and Dan Oh