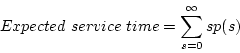Queueing Systems

• General: See figure 2.1 on page 22 for an illustration of a queueing system.
• Entities: server, waiting line (queue), customers.
• State: number of customers in the system.
• Events: arrival and departure.
• Service flow: figure 2.2 on page 23 and figure 2.3 on page 24.

  Note

  • The flows are organized by the events, one for the departure event and the other for the arrival event.
  • The randomness of the events can be emulated by rolling a dice and recording its face value (so the possible inter-arrival time would be between 1 and 6).
• Tables listed 1) interarrival time 2) service time 3) various clock readings organized by customers 4) chronological ordering of events

Example 2.1: Single-Channel Queue (Single-Server Queue).

• Customers arrive at the check-out counter at random from 1 to 8 minutes apart (interarrival time between 1 and 8 minutes) (Table 2.6 on page 28)
• Service time varies from 1 to 6 minutes with distribution shown in Table 2.7 on page 28.
• Random digit assignment in the tables are used to separate different times. For example, all interarrival time are evenly distributed with a probability of 0.125. When to use 1? When to use 8? This is distincted by the random digit assignment where 1 is used if the RDA is between 1 and 125, 8 is used if RDA is between 876-1000. They have the same length in range (125).
• Running of the simulation: Is one run enough to represent the situation? The answer is 'NO'. Typically, many random runs are required to generate sufficient statistical significance.

• Result calculation:
  
  $$Average~waiting~time = \frac{total~time~customers~wait~in~queue} {total~number~of~customers} = \frac{56}{20} = 2.8 ~minutes$$
  
  

  
  

  $$Probability (customer~has~to~wait) = \frac{number~of~customers~who~wait} {total~number~of~customers} = \frac{13}{20} = 0.65$$
  
  

  
  

  $$Probability (cashier~idle) = \frac{total~idle~time} {total~run~time} = \frac{18}{86} = 0.21$$
  
  

  
  

  $$Average~service~time = \frac{total~service~time} {total~number~of~customers} = \frac{68}{20} = 3.4~minutes$$
  
  

  This can be compared with the expected service time from the service time probability distribution
  

  $$Expected~service~time = \sum_{s=0}^{\infty} s p(s)$$
  
  
  which is
  
  $$1 * 0.1 + 2 * 0.2 + 3 * 0.3 + 4 * 0.25 + 5 * 0.1 + 6 * 0.05 = 3.2$$
  
  

  
  

  $$Average~time~between~arrivals = \frac{sum~of~all~times~between~arrivals} {number~of~arrivals - 1} = \frac{82}{19} = 4.3$$
  
  

  This can be compared with expected inter-arrival time:
  

  $$E(A) = \frac{a+b} {2} = \frac{1 + 8} {2} = 4.5$$
  
  

  The longer the simulation, the closer to their expected values (this is an indication of the quality of the random number generators).

  
  

  $$Average~waiting~time = \frac{total~time~customers~wait~in~queue} {total~number~of~customers} = \frac{56}{13} = 4.3$$
  
  

  
  

  $$Average~time~a~customer~in~system = \frac{total~time~customers~in~queue} {total~number~of~customers} = \frac{124} {20} = 6.2$$
  
  

  Note: typo on page 30, third equation: it should read ``total idle time ...'', rather than ``total run time ...''.

Example 2.2: The Able Baker carhop problem

The first example involves one server (one cashier). This example will show the case for two servers, one serves faster than the other.

If both servers are idle when a new customer comes in, Able gets the work.

A few statistics:

• The total elapse time is 62 minutes.
• Able was busy 90% of the time.
• Baker was busy 69% of the time.
• Nine out of the 26 arrivals (about 35%) had to wait. Average waiting time for all customers is about 0.42 minutes.
• Those nine, who actually waited, only waited an average of 1.22 minutes.
• Adding another server can probably reduce the waiting time to zero, but it will not be very economic.