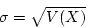- Random variable: A variable that assumes values in a irregular pattern (or
no particular pattern).
- Discrete random variables: Let X be a random variable. If the number of
possible values of X is finite, or countably infinite, X is called a discrete
random variable.
Let 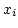 be all possible values of X, and
be all possible values of X, and
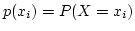 be the probability that
be the probability that
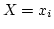 , then
, then 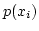 must meet the following conditions.
must meet the following conditions.
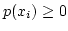 for all
for all 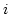 .
.
-
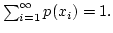
Examples: example 6.1 and 6.2 on p. 186
- Contineous random variables: If the values of X is an interval or a collection
of intervals, then X is called a contineous random variable.
For contineous random variable, its probability is represented as
The function 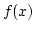 is called the probability density function (pdf) of the random variable
is called the probability density function (pdf) of the random variable 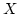 ,
which has to meet the following condition.
,
which has to meet the following condition.
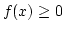 for all
for all 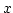 .
.
-
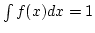 .
.
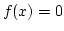 if
if 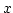 is not in
is not in 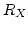 .
.
Example 6.3 on page 187.
- Cumulative distribution function. The cumulative distribution function (cdf),
denoted by
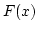 , measures the probability that the random variable
, measures the probability that the random variable 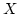 assumes a value
less than or equal to
assumes a value
less than or equal to 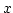 ,
,
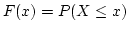 .
.
- If
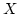 is discrete, then
is discrete, then
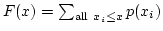
- If
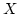 is contineous, the
is contineous, the
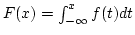
Some propertities of cdf include:
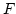 is a non-decreasing function. If
is a non-decreasing function. If 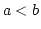 then
then 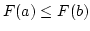 .
.
-
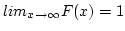 .
.
-
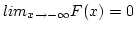 .
.
Example: 6.4, 6.5 on page 189.
- Expectation and variance. Expectation essentially is the expected value
of a random variable. Variance is a measure how a random variable varies from its expected
value.
- For discrete random variables
- For continueous random variables
- For discrete or continueous random variables, its variance is
which has an identity
- A more frequently used practical measure is standard deviation of
a random variable, which is expressed as the same units as that of expectation.
Examples: 6.6, 6.7 on page 191.
- The mode. The mode is used to describe most frequently occured values
in discreate random variable, or the maximum value of a continueous random variable.
![]() be all possible values of X, and
be all possible values of X, and
![]() be the probability that
be the probability that
![]() , then
, then ![]() must meet the following conditions.
must meet the following conditions.
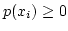 for all
for all 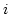 .
.
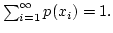
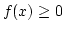 for all
for all 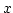 .
.
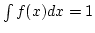 .
.
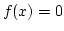 if
if 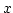 is not in
is not in 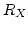 .
.
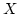 is discrete, then
is discrete, then
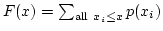
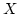 is contineous, the
is contineous, the
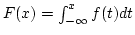
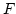 is a non-decreasing function. If
is a non-decreasing function. If 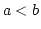 then
then 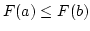 .
.
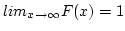 .
.
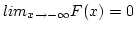 .
.
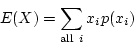
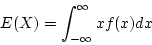
![\begin{displaymath}V(X) = E[(X - E[X])^2] \end{displaymath}](img48.png)
![\begin{displaymath}V(X) = E(X^2) - [E(X)]^2 \end{displaymath}](img49.png)