- pdf:
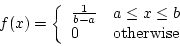
- cdf:
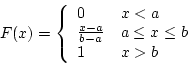
- mean:
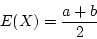
- variance:
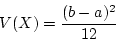
- the interval where
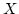 can assume value can be arbitrarily long, but
it cannot be infinite.
can assume value can be arbitrarily long, but
it cannot be infinite.
- Example 6.15 and 6.16 on page 202, 203
- pdf
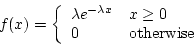
- cdf
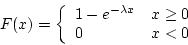
- mean
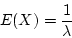
- variance
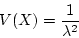
- memoryless property of the exponential distributed random variables: the future
values of the exponentially distributed values are not affected by the past values. Compare this
to, for example, a uniformly distributed random variable, one can see the difference. For example,
when throwing a fair coin, we can consider the probability of head and tail is the same which
has the value of 0.5. If, after a result of head, we would expect to see a tail (though
it may not happen). In exponentially distributed random variable, we cannot have this type
of expectation. In another word, we know nothing about the future value of the random variable
given a full history of the past.
Mathematical proof.
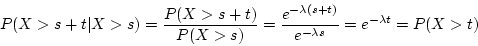
- Example 6.17 and 6.18 on page 204 and 205 where Example 6.18 demonstrates the memoryless property of the exponential distribution.
- pdf
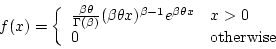
where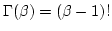 when
when 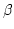 is an integer.
is an integer.
- When
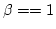 , this is the exponential distribution. In another word,
the Gamma distribution is a more general form of exponential distribution.
, this is the exponential distribution. In another word,
the Gamma distribution is a more general form of exponential distribution.
- mean
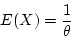
- variance
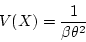
- When the parameter
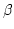 in Gamma distribution is an integer, the distribution
is refered to as Erlang distribution.
in Gamma distribution is an integer, the distribution
is refered to as Erlang distribution.
- When
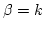 , a positive integer, the cdf of Erlang distribution is (using
integration by parts)
, a positive integer, the cdf of Erlang distribution is (using
integration by parts)
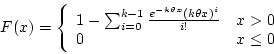
which is the sum of Poisson terms with mean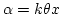
- mean
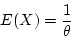
- variance
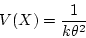
- Example 6.19, 6.20 on page 208, 209.
- pdf
![\begin{displaymath}f(x) = \frac{1}{\sigma \sqrt{2 \pi}} exp\left[ - \frac{1}{2} ...
...eft(\frac{x-\mu}{\sigma}\right)^2\right], -\infty < x < \infty \end{displaymath}](img96.png)
- cdf
![\begin{displaymath}F(x) = P(X \le x) = \int_{-\infty}^x \frac{1}{\sqrt{2\pi}} ex...
...\frac{1}{2}
\left( \frac{t - \mu}{\sigma} \right)^2 \right] dt \end{displaymath}](img97.png)
This value is very difficult to calculate. Often a table is made for
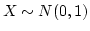 . Because
an
. Because
an
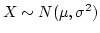 can be transformed into
can be transformed into 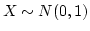 by let
by let
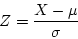
- To calculate
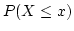 for
for
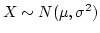 , we use
, we use
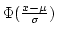
Example: to calculate F(56) for N(50,9), we have
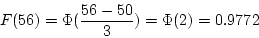
- mean
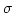
- variance
- Notation:
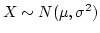
- The curve shape of the normal pdf is like a "bell".
- properties:
-
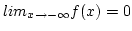 and
and
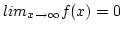
-
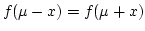 the pdf is symmetric about
the pdf is symmetric about 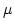 because of this,
because of this,
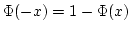 .
.
- the maximum value of the pdf occurs at
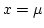 (thus, the mean and the
mode are equal.
(thus, the mean and the
mode are equal.
-
- Example 6.21 and 6.22 on page 211, 6.23 and 6.24 on page 213.
![\begin{displaymath}f(x) = \left\{ \begin{array}{ll}
\frac{\beta}{\alpha} \left( ...
...ht] & x \ge \gamma \\
0 & \rm {otherwise}
\end{array} \right. \end{displaymath}](img112.png)
- Weibull distribution has the following three parameters:
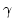 which has the range of
which has the range of
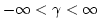 which is the
location parameter
which is the
location parameter
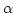 which is greater than zero which is the scale parameter
which is greater than zero which is the scale parameter
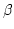 which is a positive value determines the shape
which is a positive value determines the shape