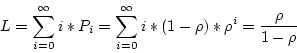In a queueing system, if the service time and inter-arrival time are
both expoentially distributed, denoted by ![]() and
and ![]() respectively plus
respectively plus
Let ![]() represent the probability the system has i customers
(including the ones in queue and ones in server).
represent the probability the system has i customers
(including the ones in queue and ones in server).
Using the principle that the flow into a state is balanced by the flow out of the state, we have
| = | ||
| ... |
solve this system of equations we get
Using the relation
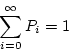
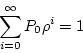
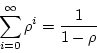
The meaning of the probability with no customer in the system is the
same as the server is idle. So the measure ![]() can be considered as
the probability that the server is busy, which is the utilization of
the server. With
can be considered as
the probability that the server is busy, which is the utilization of
the server. With ![]() solved, all other items can be solved.
solved, all other items can be solved.
Use ![]() s, we can obtain all other measures of interest.
s, we can obtain all other measures of interest.