-
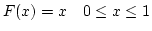
-

- As N becomes larger,
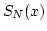 should be close
to F(x)
should be close
to F(x)
- Kolmogorov-Smirnov test is based on the statistic
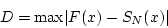
that is the absolute value of the differences. - Here D is a random variable, its sampling distribution is tabulated in Table A.8.
- If the calcualted D value is greater than the
ones listed in the Table, the hypothesis (no disagreement between the
samples and the theoretical value) should be rejected; otherwise, we
don't have enough information to reject it.
- Following steps are taken to perform the test.
- Rank the data from smallest to largest
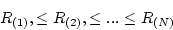
- Compute
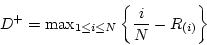
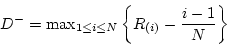
- Compute
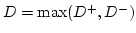
- Determine the critical value,
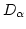 , from
Table A.8 for the specified significance level
, from
Table A.8 for the specified significance level 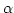 and the given
sample size N.
and the given
sample size N.
- If the sample statistic D is greater than
the critical value
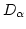 , the null hypothsis that the sample data
is from a uniform distribution is rejected; if
, the null hypothsis that the sample data
is from a uniform distribution is rejected; if
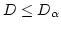 , then
there is no evidence to reject it.
, then
there is no evidence to reject it.
- Rank the data from smallest to largest
- Example 8.6 on page 300.
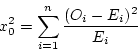
where n is the number of classes (e.g. intervals),
See Example 8.7 on page 302.