- Step 1.
- Compute the cdf of the desired random variable
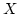 .
.
For the exponential distribution, the cdf is
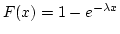 .
.
- Step 2.
- Set R = F(X) on the range of
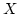 .
.
For the exponential distribution,
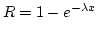 on the
range of
on the
range of 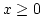 .
.
- Step 3.
- Solve the equation F(X) = R for
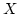 in terms of
in terms of
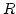 .
.
For the exponential distribution, the solution proceeds as follows.
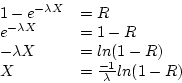
- Step 4.
- Generate (as needed) uniform random numbers
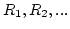 and compute the desired random variates by
and compute the desired random variates by
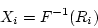
In the case of exponential distribution
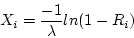
for i = 1, 2, 3, ... where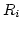 is a uniformly distributed random
number on (0,1).
is a uniformly distributed random
number on (0,1).
In practice, since both
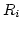 AND
AND 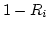 are uniformly distributed random
number, so the calculation can be simplified as
are uniformly distributed random
number, so the calculation can be simplified as
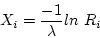
and
Because ![]() is equivelant to
is equivelant to
![]() , and
, and ![]() is a non-decreasing function (so that if
is a non-decreasing function (so that if ![]() then
then ![]() )
we get
)
we get ![]() is equivelant to
is equivelant to
![]() , which implies
that
, which implies
that
![]() which is equivelant to
which is equivelant to
![]() .
.
This means
Since
which means
This says the