Example 9.4 on page 336.
- pdf
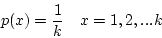
- cdf
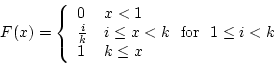
- Let F(X) = R
- Solve X in terms of R. Since x is discrete,
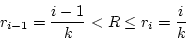
thus,
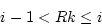
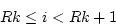
Consider the fact that i and k are integers and R is between (0,1). For the above relation to hold, we need
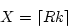
- For example, to generate a random variate X, uniformly
distributed on {1, 2, ..., 10 } (thus k = 10)
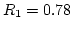
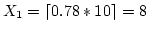
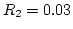
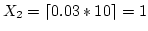
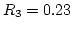
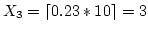
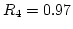
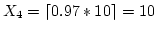
- pmf
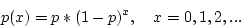
where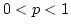
- cdf
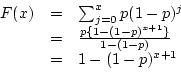
- Let R = F(x), solve for x in term of R.
Because this is a discrete random variate, use the inequality (9.12)
on page 337,
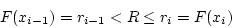
that is
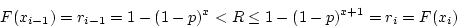
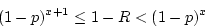
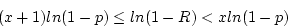
Notice that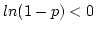
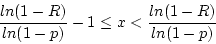
Consider that x must be an integer, so
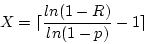
- Let
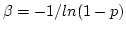 the equation above becomes
the equation above becomes
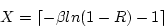
The item in the ceiling function before subtracting one is the function to generate exponentially distributed variate. - Thus one way to generate geometric distribution is
to
- let
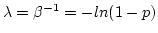 as the
parameter to the exponential distribution,
as the
parameter to the exponential distribution,
- generate an exponentially distributed variate
by
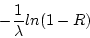
- subtract one and take the ceiling
- let
- Example 9.8 on page 341