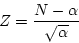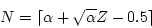Next: Input Modeling
Up: Random Variate Generation
Previous: Convolution Method
- Example: use following steps to generate uniformly distributed
random numbers between 1/4 and 1.
- Step 1.
- Generate a random number R
- Step 2a.
- If
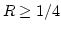 , accept X = R, goto Step 3
, accept X = R, goto Step 3
- Step 2b.
- If
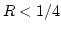 , reject R, return to Step 1
, reject R, return to Step 1
- Step 3.
- If another uniform random variate on [1/4, 1] is
needed, repeat the procedure begining at Step 1. Otherwise stop.
- Do we know if the random variate generated using above methods is
indeed uniformly distributed over [1/4, 1]? The answer is Yes. To
prove this, use the definition. Take any
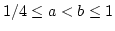 ,
,
which is the correct probability for a uniform distribution on [1/4,1].
- The efficiency: use this method in this particular example,
the rejection probability is 1/4 on the average for each number
generated. The number of rejections is a geometrically
distributed random variable with probability of ``success''
being p = 3/4, mean number of rejections is (1/p - 1)
= 4/3 - 1 = 1/3 (i.e. 1/3 waste).
- For this reason, the inverse transform (X = 1/4 + (3/4) R)
is more efficient method.
- Poisson Distribution
- pmf
where N can be interpreted as the number of arrivals in one unit time.
- From the original Poisson process definition, we know the
interarrival time
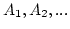 are exponentially distributed with
a mean of
are exponentially distributed with
a mean of 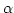 , i.e.
, i.e.  arrivals in one unit time.
arrivals in one unit time.
- Relation between the two distribution:
if and only if
essentially this means if there are n arrivals in one unit time,
the sum of interarrival time of the past n observations has to be
less than or equal to one, but if one more interarrival time is added,
it is greater then one (unit time).
- The
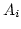 s in the relation can be generated from uniformly
distributed random number
s in the relation can be generated from uniformly
distributed random number
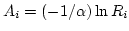 , thus
, thus
both sides are multiplied by 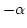
that is
- Now we can use the Acceptance-Reject method to generate Poisson
distribution.
- Step 1.
- Set n = 0, P = 1.
- Step 2.
- Generate a random number
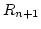 and replace P
by
and replace P
by 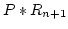 .
.
- Step 3.
- If
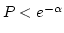 , then accept N = n, meaning
at this time unit, there are n arrivals. Otherwise, reject
the current n, increase n by one, return to Step 2.
, then accept N = n, meaning
at this time unit, there are n arrivals. Otherwise, reject
the current n, increase n by one, return to Step 2.
- Efficiency: How many random numbers will be required, on the average,
to generate one Poisson variate, N? If N = n, then n+1
random numbers are required (because of the (n+1) random numbers product).
- Example 9.10 on page 346, Example 9.11 on page 347
- When
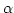 is large, say
is large, say 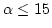 , the acceptance-rejection
technique described here becomes too expensive. Use normal distribution
to approximate Poisson distribution. When
, the acceptance-rejection
technique described here becomes too expensive. Use normal distribution
to approximate Poisson distribution. When 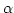 is large
is large
is approximately normally distributed with mean 0 and variance 1, thus
can be used to generate Poisson random variate.



Next: Input Modeling
Up: Random Variate Generation
Previous: Convolution Method
Meng Xiannong
2002-10-18
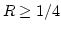 , accept X = R, goto Step 3
, accept X = R, goto Step 3
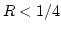 , reject R, return to Step 1
, reject R, return to Step 1
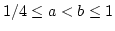 ,
,
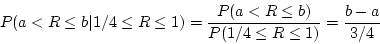
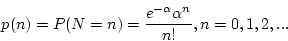
 are exponentially distributed with
a mean of
are exponentially distributed with
a mean of  , i.e.
, i.e. 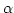 arrivals in one unit time.
arrivals in one unit time.
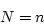
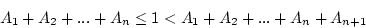
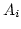 s in the relation can be generated from uniformly
distributed random number
s in the relation can be generated from uniformly
distributed random number
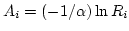 , thus
, thus
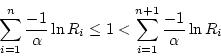
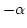
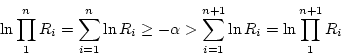
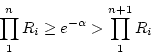
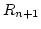 and replace P
by
and replace P
by 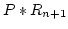 .
.
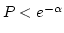 , then accept N = n, meaning
at this time unit, there are n arrivals. Otherwise, reject
the current n, increase n by one, return to Step 2.
, then accept N = n, meaning
at this time unit, there are n arrivals. Otherwise, reject
the current n, increase n by one, return to Step 2.
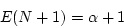
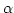 is large, say
is large, say 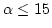 , the acceptance-rejection
technique described here becomes too expensive. Use normal distribution
to approximate Poisson distribution. When
, the acceptance-rejection
technique described here becomes too expensive. Use normal distribution
to approximate Poisson distribution. When 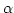 is large
is large