


Next: Goodness-of-Fit Tests
Up: Identifying the Distribution with
Previous: Quantile-Quantile Plots
- After a family of distribution has been selected such as
Poisson, Normal, Geometric ..., the next step is to estimate the
parameters of the distribution.
- Sample mean and sample variance can be used to estimate the
parameters in a distribution.
- Let
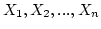 be the sample of size n.
be the sample of size n.
- The sample mean is
- The sample variance is
- If the data are discrete and grouped in a frequency
distribution, then we can re-write the equations as
and
- Example 10.5 on page 368
- If the data are continuous, we ``discretize'' them and
estimate the mean
and the variance
where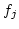 is the observed frequency in the jth class interval,
is the observed frequency in the jth class interval,
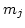 is the midpoint of the jth interval, and c is the
number of class intervals.
is the midpoint of the jth interval, and c is the
number of class intervals.
- Example 10.6 on page 369
- A few well-established, suggested estimators are listed in
Table 10.3 on page 370, followed by examples. They come from theory of
statistics.
- The examples include Poisson Distribution, Uniform Distribution,
Normal Distribution, Exponential Distribution, and Weibull Distribution.



Next: Goodness-of-Fit Tests
Up: Identifying the Distribution with
Previous: Quantile-Quantile Plots
Meng Xiannong
2002-10-18
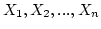 be the sample of size n.
be the sample of size n.
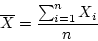
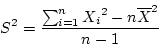
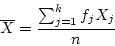
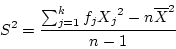
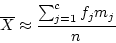
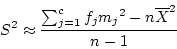
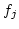 is the observed frequency in the jth class interval,
is the observed frequency in the jth class interval,
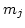 is the midpoint of the jth interval, and c is the
number of class intervals.
is the midpoint of the jth interval, and c is the
number of class intervals.