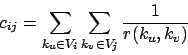Written Assignment Three
CSCI 379.01 - Information Retrieval and Web Search
Assigned: October 22nd, 2003, Wednesday
Due: October 27th, 2003, Monday
This assignment is designed for you to get familiar with some other
similarity measures other than the inner product measure and cosine
similarity measure.
- Association matrix. An association matrix is
a matrix
of n by n consisting of entries measuring the
closeness of indexing terms in their frequencies of
co-appearance. Assume there are a total of n unique terms in
the document collection, then an association matrix would look as
follows.
| |
 |
 |
...... |
 |
|
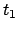 |
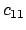 |
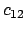 |
...... |
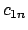 |
|
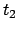 |
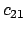 |
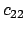 |
...... |
|
|
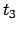 |
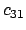 |
|
...... |
|
|
| |
|
|
|
|
|
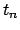 |
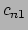 |
|
|
|
|
where each of the 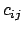 is the correlation factor between term
is the correlation factor between term 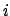 and term
and term 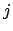 .
.
where 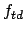 is the frequency of term
is the frequency of term 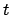 in document
in document 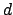 .
.
Given the following 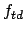 's, please compute
's, please compute 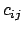 . Note that the
matrix is symmetric, so you only need to compute a half of it. Assume we
have three documents and four terms.
. Note that the
matrix is symmetric, so you only need to compute a half of it. Assume we
have three documents and four terms.
- Normalized association matrix. One problem with regular
association matrix is that it favors long documents that have many
terms and a term may appear many more times. One way to counter this
factor is to normalize the association matrix so that the value of
the matrix entries will be between 0 and 1.
Using the information in Problem 1, compute the normalized
association matrix.
- Metric correlation matrix. Association correlation does
not account for the proximity of terms in documents, just
co-occurrence frequencies within documents. Metric correlations
account for term proximity (distance between the two terms).
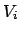 : Set of all occurrences of term
: Set of all occurrences of term 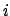 in any document.
in any document.
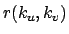 : Distance in words between word occurrences
: Distance in words between word occurrences 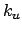 and
and
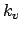 (
(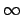 if
if 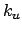 and
and 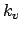 are occurrences in different
documents).
are occurrences in different
documents).
Assume a document collection contains the following two documents
only, compute the metric correlation matrix. Note that the
matrix is symmetric so you only need to compute a half of it.
Document 1:
Higher education in Pennsylvania.
Document 2:
University of Pennsylvania is a fine higher education institute.
You should ignore the stopwords in, of, is, a.
Written Assignment Three
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -nonavigation -split 1 hw3
The translation was initiated by Meng Xiannong on 2003-10-22
Meng Xiannong
2003-10-22
![]() is the correlation factor between term
is the correlation factor between term ![]() and term
and term ![]() .
.
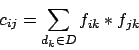
![]() 's, please compute
's, please compute ![]() . Note that the
matrix is symmetric, so you only need to compute a half of it. Assume we
have three documents and four terms.
. Note that the
matrix is symmetric, so you only need to compute a half of it. Assume we
have three documents and four terms.