Written Assignment Four

CSCI 379.01 - Information Retrieval and Web Search

Assigned: November 5yh, 2003, Wednesday
Due: November 7th, 2003, Friday

This assignment is designed for you to get familiar with the concepts of hubs and authorities using the HITS algorithm, and the PageRank algorithm.

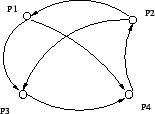
Given the following four web pages and their reference links, compute the first two rounds the following algorithms. Show the results and the steps of computation. If you use programs or spreadsheets, show the formula and results here besides submitting the programs or the spreadsheets to me.

**Figure 1:** Configuration of the four web pages
$\begin{figure}\centering\epsfysize =1in\epsfbox{hw4.eps}\end{figure}$

The HITS algorithm for hubs and authorities.
Initialize for all $p \in S$ :
For i = 1 to numOfSteps do
      For all $p \in S: a_p = \sum_{q:q\rightarrow p} h_q$
      For all $p \in S: h_p = \sum_{q:p\rightarrow q} a_q$
      For all $p \in S: a_p = a_p / c$ where $\sum_{p\in S} (a_p/c)^2 = 1$
      For all $p \in S: h_p = h_p / c$ where $\sum_{p\in S} (h_p/c)^2 = 1$
The PageRank algorithm for page ranks.
Let be the total set of pages.
Let $\forall p \in S: E(p) = \alpha / \vert S\vert$ (e.g. $\alpha = 0.15$ )
Initialize $\forall p \in S: R(p) = 1/\vert S\vert$
Until ranks do not change (much)
      for each $p \in S$ :
              $R'(p) = \sum_{q: q\rightarrow p} \frac{R(q)}{N_q} ~~ + E(p)$
       $c = 1 / \sum_{p \in S} R'(p)$
      for each $p \in S: R(p) = c * R'(p)$