


Next: Generation of Pseudo-Random Numbers
Up: Random-Number Generation
Previous: Random-Number Generation
- A sequence of random numbers,
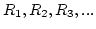 must have
two important properties:
must have
two important properties:
- uniformity, i.e. they are equally probable every
where
- independence, i.e. the current value of a random
variable has no relation with the previous values
- Each random number
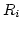 is an independent sample drawn from a
continueous uniform distribution between zero and one.
is an independent sample drawn from a
continueous uniform distribution between zero and one.
- Some consequences of the uniformity and independence
properties
- If the interval (0,1) is divided into n
sub-intervals of equal length, the expected number of observations in
each interval is N/n where N is the total number of
observations. Note that N has to be sufficiently large to show
this trend.
- The probability of observing a value in a particular
interval is independent of the previous values drawn.
Meng Xiannong
2002-10-18
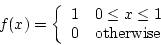
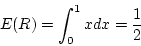
![\begin{displaymath}V(R) = \int_0^1 x^2 dx - [E(R)]^2 = \frac{1}{12} \end{displaymath}](img150.png)