Linear Congruential Method

• The linear congruential method produces a sequence of integers $X_1, X_2, X_3, ...$ between zero and m-1 according to the following recursive relationship:
  
  $$X_{i+1} = (a X_i + c) ~ {\rm mod} ~ m, ~~~~~~ i = 0, 1, 2, ...$$
  
  
  • The initial value 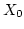$X_0$ is called the seed;
  • a is called the constant multiplier;
  • c is the increment
  • m is the modulus
  The selection of a, c, m and $X_0$ drastically affects the statistical properties such as mean and variance, and the cycle length.

• When $c \ne 0$, the form is called the mixed congruential method; When c = 0, the form is known as the multiplicative congruential method.

• Example 8.1 on page 292

• Issues to consider:
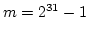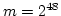  • The numbers generated from the example can only assume values from the set I = {0, 1/m, 2/m, ..., (m-1)/m}. If m is very large, it is of less problem. Values of $m = 2^{31} -1$ and $m = 2^{48}$ are in common use.
  • To achieve maximum density for a given range, proper choice of a, c, m and 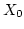$X_0$ is very important. Maximal period can be achieved by some proven selection of these values.
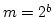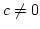    • For m a power of 2, i.e. $m = 2^b$, and $c \ne 0$, the longest possible period is 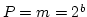$P = m = 2^b$, when c is relatively prime to m and a = 1 + 4 k where k is an integer.
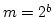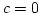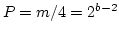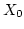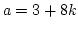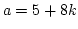    • For m a power of 2, i.e. $m = 2^b$, and $c = 0$, the longest possible period is $P = m/4 = 2^{b-2}$, when $X_0$ is odd and the multiplier, a is given by $a = 3 + 8 k$ or $a = 5 + 8 k$ where k is an integer.
    • For m a prime number and c = 0, the longest possible period is P = m - 1 when a satisfies the property that the smallest k such that 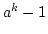$a^k - 1$ is divisible by m is k = m - 1.

      For example, we choose m = 7 and a = 3, the above conditions satisfy. Here k has to be 6.

      • when k = 6, 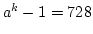$a^k - 1 = 728$ which is divisible by m
      • when k = 5, 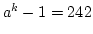$a^k - 1 = 242$ which is not divisible by m
      • when k = 4, 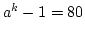$a^k - 1 = 80$ which is not divisible by m
      • when k = 3, 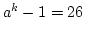$a^k - 1 = 26$ which is not divisible by m
      Of course, the longest possible period here is 6, which is of no practical use. But the example shows how the conditions can be checked.

• Examples 8.2, 8.3 and 8.4 on page 294 and page 295.