Bucknell Unversity Astronomy 101
Problem Set #3 Solutions

Problem #1: Consider for a moment Aristarchus' measurement of the ratio of the distance to the Moon to the distance to the Sun (this was discussed in class, and it's written up in both the class notes and your text). As we mentioned in class, Aristarchus measured an angle of 87 degrees for the elongation of the First Quarter Moon. This must've been a very tough measurement without modern equipment, and, as it turns out, his value is incorrect. What value should he have measured? Look up the average Earth-Moon and Earth-Sun distances in the back of your book, and calculate the real value of the First Quarter Moon's elongation. Please show your work, including a diagram of the Sun-Moon-Earth geometry.

Solution: OK, basically we're asked to do Aristarchus' famous measurement of the elongation of the Moon at quadrature, only this time we'll use the modern values for DSun, the distance to the Sun, and DMoon, the distance to the Moon. (If you don't remember how Aristarchus made his measurement, look at the web page for 7 September.)

Making use of the fact that when the Moon is in its First Quarter phase, the angle between the Moon-Sun line and the Moon-Earth line is 90 degrees, we can set up the following right triangle:

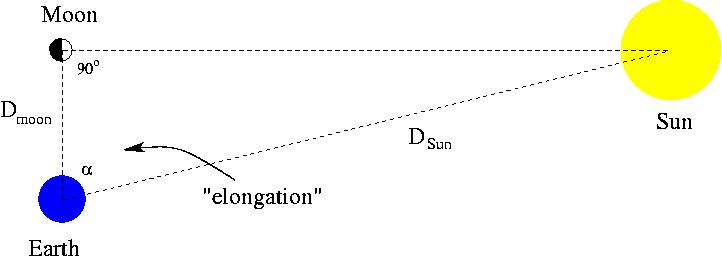
where DSun and DMoon are labeled, and alpha is the elongation of the Moon (recall that the elongation of the Moon is the angle between the Earth-Sun direction and the Earth-Moon direction).

Now, since we're dealing with a right triangle, we know that

cos(alpha) = adjacent/hypoteneuse = DMoon/DSun

and we can look up these values in the back of our book:

So,

cos(alpha) = 384.4 x 103 km / 149.6 x 106 km

Note that since your textbook author was kind enough to give us both of these terms in the same units, we don't have to mess around with any unit conversions (yeah!), and we can just divide:

cos(alpha) = 0.002570

And, using the "inverse cos" button on my calculator, I get

alpha = 89.85 degrees

Note: Be sure to have your calculator set up to express the answer in degrees. Some calculators give angles in another unit called radians. If your answer was 1.568, this is likely the problem.

Problem #2: In 1989, the Hipparcos satellite was launched. Its primary purpose was to measure the parallax of nearby stars so that their distances could be calculated. Hipparcos measured the parallax shift of stars using the method described on your Parallax special web page -- it measured the difference in the direction to nearby stars due to the Earth's motion around the Sun. The satellite, which operated for three years, was remarkably successful, and was able to measure accurate parallaxes for stars as distant as 100 parsecs away. (A "parsec" is a unit of distance; look it up in the back of your book.)

So how accurately did Hipparcos have to measure angular differences? Consider a star located 100 parsecs away. Calculate the change in the direction to the star between times separated by six months (i.e., between two different times when the Earth is on either side of the Sun in its orbit).

Solution: This one is an application of what you learned from the Parallax special web page and our discussion in class. I'll reproduce the relevant figure from the class discussion below:

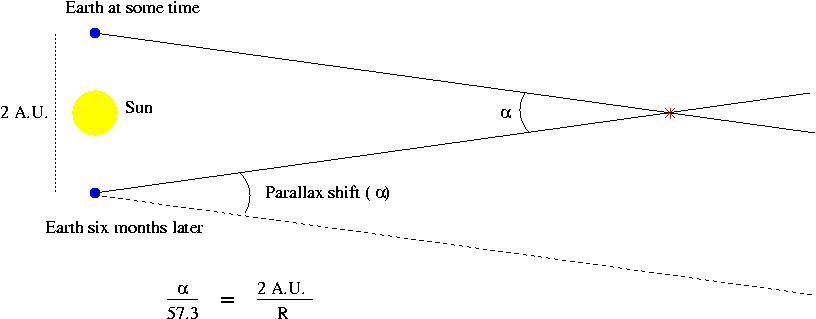
This figure shows the Earth at two different times separated by six months, in which time the Earth has moved from one side of the Sun to the other. Between these two times, our perspective has changed by 2 A.U., and the difference in the direction to the star has changed by alpha.

In class, we considered a given angle alpha, and figured out how far away the star that produces that parallax shift has to be. In this problem, we'll do the opposite. You're given the distance to the star, and asked how big a parallax shift that would produce.

In either case, we can use the Observer's Triangle relation:

alpha/57.3 = 2 A.U. / R

where R is the distance to the star. We're told that R = 100 pc, so we should be able to plug this value in and calculate alpha. However, unlike the last problem, this problem contains quantities in different units ( A. U. vs. pc), and we have to convert. In principle, you could convert from one to the other (e.g., from pc to A.U.), but to be especially clear, I'll convert both to meters. The conversion factors can be found in the back of your book.

For the distance across the Earth's orbit,

and for the distance to the star,

Therefore,

alpha/57.3 = 2.992 x 1011 m / 3.086 x 1018 m
alpha/57.3 = 9.714 x 10-8

Multiplying both sides by 57.3, I get

alpha = 57.3 x 9.714 x 10-8 = 5.56 x 10-6 degrees.

Converting this to arcseconds (just for fun), this is

alpha = 5.56 x 10-6 degrees x (3600 arcsec/ 1 degree) = 0.02 arcsec

The best telescopes on Earth can measure angles to about 1 arcsecond. To get to this absurdly high measurement accuracy, the Hipparcos satellite had to be put in space, above the blurring effects of the Earth's atmosphere.

Note on significant figures: It's hard to say how many significant figures to keep, because I was unclear about the number of significant figures in the quoted distance of 100 pc. It seems to me that plausible choices are 1 significant figure (i.e., 1 x 102 pc), or 3 significant figures (i.e., 1.00 x 102 pc). As long as you didn't give me way too many significant figures, I didn't deduct points.

Problem #3: I keep saying in class that the idea of a rotating Earth orbiting the Sun is preposterous, because such an idea implies that we're moving through space at an enormous speed. Let's see if we can quantify just what kind of speeds we're talking about here.

a) Let's do this in two parts. First, we'll consider how fast we're moving because of the rotation of the Earth on its axis. To make the problem easier, let's assume we live on the Equator. Based on the fact that the Earth rotates once in a day (what kind of day?), we can calculate how fast a person on the Equator is moving. Do it.

b) Now let's figure out how fast the Earth moves in its orbit around the Sun. How long does it take for the Earth to take one lap around the Sun? And how far is that? Answer these questions and you should be able to figure out how fast the whole planet moves in its orbit. Do it.

c) Lastly, let's compare these speeds to speeds of everyday things. How many times faster than a speeding car (say, at 65 mph) is our planet rotating and orbiting? (It may help to remember from lab that 1 m/s = 2.24 mph).

Solution: A lot of you get hung up in the concept of speed, and I think if you just stop worrying about what the "formula" for speed is, you'll realize that speed is a very intuitive concept. Whether it be measured in meters/second of miles/hour, speed is simply how fast something moves. Quantifying that just means figuring out how long it takes for that object to move over a known distance. Which distance doesn't really matter -- if you're measuring a speed, you just need to know how long it takes to cover any measured distance. Distance and time -- that's all you need.

For part a), we need the distance someone on the Equator travels in a specified time. The most obvious time to me is the time it takes for the Earth to spin once on its axis -- that's a sidereal day. Below is a cutaway diagram of the Earth (i.e., a slice through the Earth), but this time, I've made the cut along the Equator.

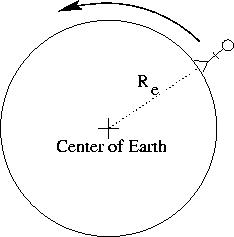
From this picture, it should be clear that a person on the Eqautor will travel around in a circle whose radius is the radius of the Earth (Re) in a sidereal day. Recalling that the circumference of a circle is 2 pi times its radius, we get:

where I found the radius of the Earth in the back of my textbook. What's the time it takes for a person to do this? It's a sidereal day:

So the speed is nothing more than distance/time, or

To some of you, this might look like a small number, but realize that traveling 1 km/s means getting from here to the Freez in 1 second. Incidentally, we don't travel quite that fast up here at 41 degrees latitude, because as the Earth rotates, we trace out a smaller circle (look at a globe, an you'll see). Our speed is about 75% of that of an Equator-dweller.

For part b), We'll do the same thing, only here the distances and times are different. The Earth makes one trip around the Sun in a year, and it travels in a circle whose radius is equal to the distance between the Earth and Sun (Ro in the picture below).

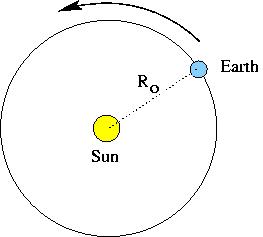
Let's start with the total distance traveled. From the back of the book, I find that the distance between Earth and Sun is one Astronomical Unit, or A.U. for short. Its value in kilometers is:

This is the distance between the Earth and Sun, not the distance the Earth travels in its orbit. That would be the circumference of the circle, or OK so that's the distance traveled in one year. We should probably convert one year into units of seconds, so that our speed will have units of km/s, so Now, speed is distance/time, so Note that this speed is way bigger than the speed of rotation found in part a) above.

In part c), I just ask you to compare these speeds with a speed that you have some intuitive grasp of -- like the speed of a car on the highway. In order to do a comparison, though, we'll need convert the miles/hour units to m/s or km/s. Luckily for you. I gave you the conversion factor:

Note that in the last two lines, I converted to units of km/s, since my values above are in these units.

Now, to compare the speeds in parts a) and b) above, we just divide those speeds by the car's speed. This will give us how many times the speed of a car these other speeds are:

so the speed of a person on the Equator is 16 times the speed of a car on the highway.

Likewise, we can calculate how many times the speed of a car the speed of the Earth in its orbit is:

so the speed of the Earth in its orbit is 1024 times the speed of a car on the highway.