In this lab, we will experiment with useful circuits that use the operational amplifier (op amp). In particular, we will look at a summing amplifier and its use in a digital-to-analog (D/A) conversion circuit.

The goals in this lab are to gain a better understanding of how op amp circuits work, as well as to wire and test the circuits. Some parts of this lab assignment ask you to analyze a circuit. Please include that analysis in your lab notebook, and briefly discuss your analysis with the lab instructor before wiring the circuits.

Please bring the Bobrow textbook to lab on February 17.

Also, do the following pre-lab activities before arriving to lab on February 17.

• Items 1 and 2 in Section 1. Try to understand why the resistors in the inverting amplifier circuit are usually chosen larger than 1,000 ohms.
• Item 1 in Section 2.

Please do the following pre-lab activity before arriving to lab on February 24:

Complete the analysis of the R-2R D/A conversion circuit in Section 3, item 5. Show all of the details in your lab notebook, using the superposition approach that we discussed in lecture on February 18. Then, choose appropriate resistor values so that your circuit will operate according to the truth table in Section 3, item 6.

1. Inverting Amplifier

Consider the inverting amplifier circuit shown in Figure 2.15 on page 75 of the Bobrow text. This is the circuit that you constructed in Lab 4.
1. Repeat the analysis that leads to the result that the output voltage v_o is related to the input voltage v_s according to v_o = -(R₂ / R₁) v_s.

   For your convenience, the inverting amplifier circuit shown in Figure 2.15 of the Bobrow text is shown in Figure 1 below. The notation in Figure 1 is slightly different from the text, so the equation describing Figure 1 is .

   

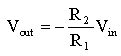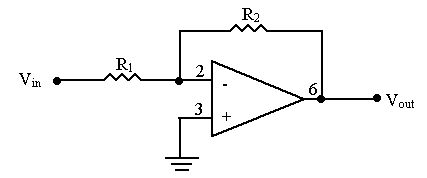
   Figure 1: "Inverting amplifier" with 741 op amp.

2. Suppose you want to design an inverting amplifier with gain = -(R₂ / R₁) = -10. Ideally, any resistor values that satisfy R₂ = 10 R₁ will work. However, with real op amp circuits, the resistor values need to be chosen with some care. What would be different in the circuit if R₁ = 1 ohm, R₂ = 10 ohm versus R₁ = 1 k ohm, R₂ = 10 k ohm?

   Look at the data sheet for the National Semiconductor LM 741 Op Amp, which is available on the Web at http://www.national.com/pf/LM/LM741.html
   What is the maximum current that the 741 op amp can provide into and out of its output terminal? In order to satisfy this limitation, what size resistors should be chosen for R₁ and R₂?

3. Do you have any questions about the inverting amplifier circuit that you constructed in Lab 4?

2. A Summing Amplifier

Many applications require that two or more signals be added while also being amplified. This need arises frequently in audio systems. For example, in a music performance, we might have several microphones, each connected to a different singer or instrument. A "mixing panel" is usually available that allows each microphone signal to be amplified separately before being added and sent to the speakers.

An op amp circuit that amplifies and adds signals is shown in Figure 2.17 on page 77 of the text. Let us generalize the circuit slightly by replacing the resistors R₁ by different resistors R_a and R_b connected to the input sources v_a and v_b, respectively.

1. Show that v_o = -(R₂ / R_a) v_a -(R₂ / R_b) v_b. Does this circuit amplify and add two voltages?

2. Design an inverting, summing amplifier whose output voltage is the negative average of the two input voltages. Record your design in your notebook, and demonstrate the circuit operation to the lab instructor. Are there any limitations on the size of the input signals so that the circuit correctly outputs the negative average?

3. Explain how two potentiometers can be used to provide an "audio mixer" for two microphones with variable gains. Demonstrate the mixer circuit.

3. Digital-to-Analog Conversion

A digital-to-analog (D/A) conversion circuit is needed in any system that produces an analog output signal (voltage) based on inputs that are digital (0's and 1's or binary). An example that all of us are familiar with is the audio compact disk (CD). The music is digitally encoded on the CD, but your CD player converts the 0's and 1's into an analog music signal that is played through your speakers.

Let us consider a 3-bit D/A converter. A binary (base 2) number with 3 bits b₂b₁b₀ is equivalent to the decimal (base 10) number 2² b₂ + 2¹ b₁ + 2⁰ b₀ = 4 b₂ + 2 b₁ + b₀. For example, the binary number 110 is equivalent to the decimal number 6.

Use the summing amplifier studied in the previous section to design a 3-bit D/A conversion circuit. Assume that a binary '0' is represented by a 0 volt source, while a binary '1' is represented by a +5 volt source. Pages 891-893 in the text discuss D/A conversion. The circuit in Figure 13.37 will be useful, if you take the output after the first op amp at v₁. With reference to Figure 13.37, your D/A converter should operate as follows.

    A2    A1    A0      Output voltage v1
    --    --    --      -----------------

    0V    0V    0V       0 V
    0V    0V   +5V      -1 V
    0V   +5V    0V      -2 V
    0V   +5V   +5V      -3 V
   +5V    0V    0V      -4 V
   +5V    0V   +5V      -5 V
   +5V   +5V    0V      -6 V
   +5V   +5V   +5V      -7 V

Please do the following activities.
1. Design the D/A converter, specifying all resistor values and explaining your reasoning.

2. Build the circuit and demonstrate that it operates properly.

3. The D/A converter in a CD player must convert 16-bit binary numbers to analog voltage values. If you were to extend your design to 16 bits with the output voltage level between 0 V and -10 V, which resistor values would be needed in your circuit?

4. The D/A converter in Figure 13.38 of the text uses an R-2R ladder. Why is this design better than your previous design, particularly if you extend to 16 bits?

5. Do your best to explain the analysis of the R-2R ladder D/A converter that is presented on page 893 of the text. Try to explain the analysis to the lab instructor. The analysis uses the principle of superposition and facts about combinations of series and parallel resistors. Include a discussion of the operation of the circuit in your lab notebook.

6. Each student should individually design and construct a 3-bit D/A converter using an R-2R ladder, as in Figure 13.38. That is, each student should construct a circuit on their breadboard. Specify the resistor values in your lab notebook, with an explanation of your reasoning in choosing the values. Your circuit should operate according to the following table.

       A2    A1    A0      Output voltage v2
       --    --    --      -----------------
   
       0V    0V    0V       0 V
       0V    0V   +5V      +1 V
       0V   +5V    0V      +2 V
       0V   +5V   +5V      +3 V
      +5V    0V    0V      +4 V
      +5V    0V   +5V      +5 V
      +5V   +5V    0V      +6 V
      +5V   +5V   +5V      +7 V
   

   For your convenience, the circuit in Figure 13.38 is shown in Figure 3 below, with slightly different notation. The variables A₀, A₁, A₂, v₁, v₂ in Figure 13.38 correspond to V₀, V₁, V₂, V_b, V_a in Figure 3 below, respectively.
   
   
   
   
   

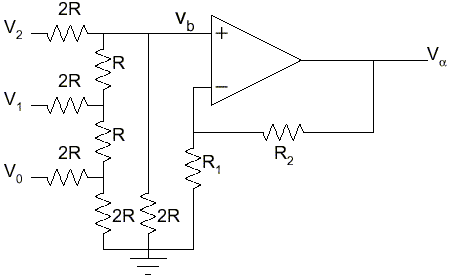
   Figure 3: A 3-bit D/A converter using an R-2R ladder.

7. Each student will individually demonstrate his/her circuit by the end of lab on February 17 or at the beginning of lab on Thursday, February 24.
   ** NOTE: We will continue to work on the R-2R ladder DAC on February 24, and all students will demonstrate their circuit by March 3.
   The purpose of having each student do this individually is to make sure that all of you are progressing in your EE lab skills. If you do not finish by the end of the lab session on February 17 ** changed to February 24 **, please wire your circuit outside of lab so that you are ready to demonstrate your circuit on February 24 ** changed to March 3 **.

8. On February 24, please hand in your lab notebook so that Labs 1-4 ** changed to Labs 1-5 ** can be graded.
   ** NOTE: The lab notebooks will be due on Thursday, March 3. **
Thank you and have fun!