- A Bernoulli trail is an experiment with result of success or failure.
- We can use a random variable to model this phenomena. Let
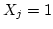 if it
is a success,
if it
is a success, 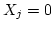 if it is a failure.
if it is a failure.
- A consecutive
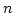 Bernoulli trails are called a Bernoulli process if
Bernoulli trails are called a Bernoulli process if
- the trails are independent of each other;
- each trail has only two possible outcomes (success or failure, true or false, etc.); and
- the probability of a success remains constant
- The following relations hold.
-
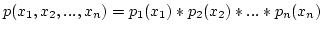 which means the probability of the result of a sequence of events is equal to the product
of the probabilities of each event.
which means the probability of the result of a sequence of events is equal to the product
of the probabilities of each event.
- Because the events are independent and the probability remains the same,
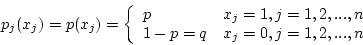
-
- Note that the "location" of the
 s don't matter. It is the count of
s don't matter. It is the count of  s
that is important.
s
that is important.
- Examples of Bernoulli trails include: a conscutive throwing of a "fair" coin, counting heads and tails; a pass or fail test on a sequence of a particular components of the "same" quality; and others of the similar type.
- For one trial, the distribution above is called the Bernoulli distribution.
The mean and the variance is as follows.
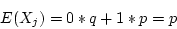
![\begin{displaymath}V(X_j) = E[X^2] - (E[X])^2 = [0^2*q + 1^2 * p] - p^2 = p (1-p) \end{displaymath}](img58.png)
- The number of successes in
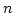 Bernoulli trials is a random variable,
Bernoulli trials is a random variable, 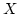 .
.
- What is the probability that
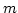 out of
out of 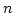 trials are success?
trials are success?
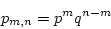
- There are
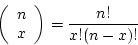
- So the total probability of
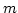 successes out of
successes out of 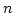 trials is given by
trials is given by
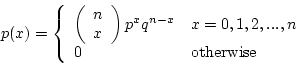
- Mean and variance: consider the binomial distribution as the sum of
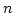 independent Bernoulli trials. Thus
independent Bernoulli trials. Thus
![\begin{displaymath}E[X] = p + p + ... + p = np \end{displaymath}](img63.png)
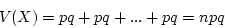
- Example 6.10 on page 198
- The number of trials needed in a Bernoulli trial to achieve the first success is a random variable that follows the geometric distribution.
- The distribution is given by
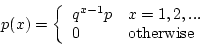
- The mean is calculated as follows.
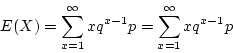
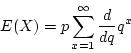
because the sequence converges, so we can exchange the order of summation and the differentiation.
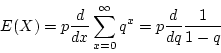
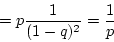
- Variance
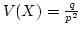
- Example 6.11 on page 199
- Poisson distribution property: mean and variance are the same
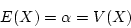
- The cdf of the Poisson distribution
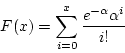
because
 is a constant and the increase rate of
is a constant and the increase rate of 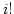 is much faster than that of
is much faster than that of
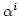 , the distribution is mostly determined by the first a few items.
, the distribution is mostly determined by the first a few items.
- Poisson distribution is most useful in Poisson process which is used most frequently in describing such phenomena as telephone call arrivals.
- Example 6.12, 6.13, 6.14 on page 200, page 201