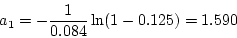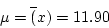Next: Verification and Validation of
Up: Input Modeling
Previous: Parameter Estimation
- Earlier we introduced hypothesis test to examine the quality
of random number generators. Now we will apply these tests to hypothesis
about distributional forms of input data.
- Goodness-of-fit tests provide helpful guidance for evaluating
the suitability of a potential input model.
- The tests depends heavily on the amount of data. If very little
data are available, the test is unlikely to reject any candidate
distribution (because not enough evidence to reject); if a lot of data
are available, the test will likely reject
all candidate distributions (because none fits perfectly).
- Failing to reject a candidate should be viewed as a piece of
evidence in favor of that choice; while rejecting an input model is
only one piece of evidence against the choice.
- Chi-square test is for large sample sizes, for both discrete
and continuous distributional assumptions, when parameters are estimated
by maximum likelihood.
- Arranging the n observations into a set of k
class intervals or cells.
- The test statistic
where 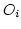 is the observed frequency in the ith class interval and
is the observed frequency in the ith class interval and
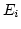 is the expected frequency in that class interval.
is the expected frequency in that class interval.
- The
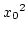 approximately follows the chi-square distribution
with k-s-1 degrees of freedom, where s represents the
number of parameters of the estimated distribution. E.g Poisson
distribution has s = 1, normal distribution has s=2.
approximately follows the chi-square distribution
with k-s-1 degrees of freedom, where s represents the
number of parameters of the estimated distribution. E.g Poisson
distribution has s = 1, normal distribution has s=2.
- The hypothesis
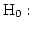
- the random variable, X, conforms
to the distributional assumption with the parameter(s) given
by the parameter estimate(s)
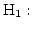
- the random variable X does not
conform the distribution
- The critical value
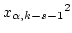 is found in Table
A.6.
is found in Table
A.6. 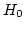 is rejected if
is rejected if
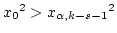 .
.
- The choice of k, the number of class intervals, see
Table 10.5 on page 377.
- Example 10.13 on page 377.
- Chi-square test with equal probabilities:
- If a continuous distributional assumption is being tested,
class intervals that are equal in probability rather than equal
in width of interval should be used.
- Example 10.14: Chi-square test for exponential distribution
(page 379)
- test with intervals of equal probability (not
necessary equal width)
- number of intervals less than or equal to n/5
- n = 50, so
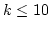 , according to recommendations
in Table 10.5, 7 to 10 class intervals be used.
, according to recommendations
in Table 10.5, 7 to 10 class intervals be used.
- Let k = 8, thus
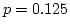
- The end points for each interval are computed from
the cdf for the exponential distribution
where 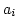 represents the end point of the ith interval.
represents the end point of the ith interval.
- Since
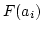 is the cumulative area from zero
to
is the cumulative area from zero
to 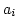 , thus
, thus 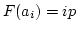
thus
regardless the value of 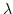 ,
, 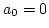 and
and 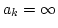 .
.
- With
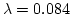 in this example and k = 8,
in this example and k = 8,
continue with i = 2,3,...,7 results in 3.425, 5.595, 8,252,
11.677, 16.503, and 24.755.
- See page 379 and 380 for completion of the example.
- Example 10.15 (Chi-square test for Weibull distribution)
on page 380
- Example 10.16 (Computing intervals for the normal distribution)
on page 381
- For the given data, using suggested estimator in Table
10.3 on page 370, we know (the original data was from Example 10.3
on page 360)
- Kolmogorov-Smirnov Goodness-of-fit test
- Chi-square test heavily depends on the class
intervals. For the same data, different grouping of the data
may result in different conclusion, rejection or acceptance.
- The K-S goodness-of-fit test is designed to overcome
this difficulty. The idea of K-S test is from q-q plot.
- The K-S test is particularly useful when sample
size are small and when no parameters have been estimated
from the data.
- Example 10.7 on page 383, using the method described
in Section 8.4.1 on page 299. A few notes:
- If the interarrival time is exponentially distributed,
the arrival times are uniformly distributed on (0,T]



Next: Verification and Validation of
Up: Input Modeling
Previous: Parameter Estimation
Meng Xiannong
2002-10-18
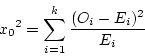
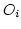 is the observed frequency in the ith class interval and
is the observed frequency in the ith class interval and
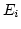 is the expected frequency in that class interval.
is the expected frequency in that class interval.
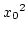 approximately follows the chi-square distribution
with k-s-1 degrees of freedom, where s represents the
number of parameters of the estimated distribution. E.g Poisson
distribution has s = 1, normal distribution has s=2.
approximately follows the chi-square distribution
with k-s-1 degrees of freedom, where s represents the
number of parameters of the estimated distribution. E.g Poisson
distribution has s = 1, normal distribution has s=2.
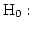
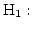
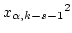 is found in Table
A.6.
is found in Table
A.6. 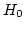 is rejected if
is rejected if
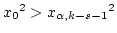 .
.
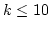 , according to recommendations
in Table 10.5, 7 to 10 class intervals be used.
, according to recommendations
in Table 10.5, 7 to 10 class intervals be used.
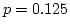
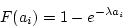
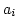 represents the end point of the ith interval.
represents the end point of the ith interval.
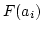 is the cumulative area from zero
to
is the cumulative area from zero
to 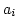 , thus
, thus 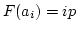
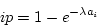
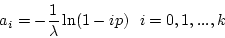
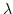 ,
, 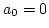 and
and 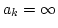 .
.
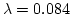 in this example and k = 8,
in this example and k = 8,